3.3 Hallov model osvetlitve

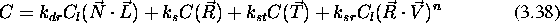
Prejsnja modela odboja svetlobe na povrsni nista upostevala svetlobe, ki prehaja skozi povrsino, kot tudi ne svetlobe, ki jo povrsine sevajo. V mnogih racunalniskih programih se barva izracunava z enacbo:

kjer je:

C
barva povrsine

barva svetlobnega izvora

enotski vektor orientacije povrsine

enotski vektor v smeri zrcalno odbite svetlobe

enotski vektor v smeri gledanja

enotski vektor v smeri lomljene svetlobe

difuzna odbojnost

zrcalna odbojnost

zrcalna prepustnost

Phongova odbojnost
n
Phongov eksponent

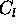
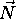
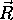
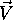
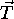
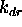
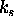
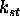
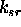
V tem modelu je predpostavljeno, da je izvor svetlobe tockast in lezi v neskoncnosti, kar omogoca uporabo konstante 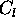na vseh vpadnih tockah. Osvetlitev okolice je potrebno upostevati v vseh konstantah izrazov. Vsak izraz podaja razlicen efekt:

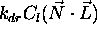
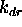Difuzno odbita svetloba. je razlicen od nic za vse matirane povrsine.

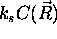
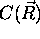Zrcalno odbita svetloba. je barva vidna v smeri 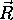, zmanjsana za zrcalno odbojnost 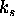. Za gladke povrsine bi se morala uporabiti le konstanta 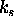, ki je razlicna od nic za vse zglajene povrsine. Ce se ne uporabi Fresnelovih enacb, bi moral biti 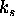vecji pri nizkih vpadnih kotih ().

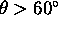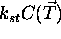
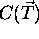Prepuscena svetloba. je barva vidna v smeri vektorja 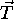, zadusena z zrcalno prepustnostjo 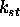. Vsota 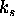in 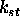naj bi bila ena.

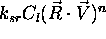
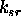Phongov izraz za odblesk. Razprsi zrcalni odboj v tocki. je izrazit na kompozitnih povrsinah.

Hallov model [HG83] dodatno deli vpadno svetlobo na dva razreda: svetloba, ki prihaja direktno iz svetlobnih izvorov in na svetlobo, ki prihaja od ostalih objektov. Potreba po taki delitvi je v tem, da je pri metodi sledenja zarka potrebno upostevati tudi svetlobo, ki jo generirajo drugi objekti. To je svetloba, ki je prisla z odbojem od povrsine ali pa skozi povrsino. V primerjavi z modelom (3.38) uposteva tudi razprsitev svetlobe pri zrcalnem prehodu, kot tudi dusenje na enoto dolzine pri prehodu svetlobe skozi prosojni material. Torej modelira vse znacilnosti interakcije svetlobe s povrsino in se zelo pribliza zahtevam po stirih nacinih prenosa svetlobe, opisanih na strani . Hallov model, kot razsiritev standardnega modela (3.38), z upostevanjem vecjega stevila svetlobnih izvorov, zapisemo v naslednji obliki:

kjer je:

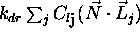
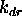Difuzni odboj svetlobe, ki je prisla iz svetlobnega izvora. Konstanta podaja difuzno sposobnost povrsine. Hrapave povrsine imajo 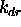blizu ena, medtem ko zrcalne povrsine nimajo difuznih lastnosti. Ker je svetlobih izvorov lahko vec, je potrebno za vsak izvor dolociti kosinus kota med izvorom svetlobe 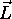in normalo povrsine 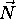. Razprsitev svetlobe torej ustreza Lambertovem zakonu.

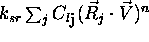
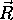Zrcalni odboj. Upostevati je potrebno vec svetlobnih izvorov. Popolni odboj ima najvecjo intenziteto v smeri odbitega vektorja . Za porazdelitev odbleska na vecje podrocje se uporablja Phongova kontrola s potenco kosinusa kota med odbitim zarkom v smeri 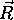in kotom gledanja 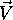. V izrazu 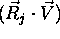se lahko uporabi tudi polovicni vektor 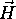(3.16), kot ustrezno merilo za .

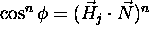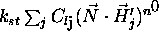
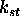Zrcalni prehod svetlobe uposteva kolicino prepuscene svetlobe iz svetlobnega izvora s konstanto . Podobno kot pri zrcalnemu odboju, je tudi tu uporabljena Phongova distribucijska funkcija, le da je tu potrebno uporabiti zrcalni vektor prehoda 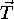. Ustrezni vektor je pri prepusceni svetlobi 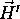, le da je tu potrebno upostevati drug kot loma svetlobe zaradi razlicnih lomnih kolicnikov dveh medijev:

 


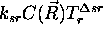
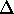Zrcalni odboj svetlobe, ki prihaja z drugih teles. Prehodnost svetlobe na enoto dolzine T, skupaj z dolzino zarka , doloca jakost absorbcije svetlobe v mediju, skozi kateri zarek potuje. Barva svetlobe v smeri zrcalnega odboja 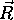se ne izracunava s porazdelitveno funkcijo, kot je to primer pri dolocanju svetlobe pri svetlobnih izvorih. Razlog je v tem, da bi bilo potrebno za svetlobo, ki prihaja iz drugih teles, pri metodi sledenja zarku, generirati vecje stevilo zarkov in ne samo enega v smeri zrcalnega odboja. Barva takega odboja se tako doloci, kot ce bi to bil popolni zrcalni odboj. Za pravilno dolocitev barve lahko tu uporabimo Fresnelovo enacbo (2.6). Prehodnost T pri medijih, kot je zrak lahko postavimo na ena in s tem ne vplivamo na slabljenje zarka.

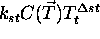
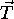Zrcalna prehodnost svetlobe, ki prihaja iz drugih teles skozi povrsino. Podobno kot pri zrcalnem odboju, tudi tu kontroliramo prepusceno sveltobo v smeri lomljene svetlobe . Absorbcija svetlobe 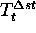je tu obicajno manjsa od ena, saj so snovi skozi katere zarek potuje najveckrat voda ali drugi materiali, ki veliko bolj slabijo svetlobo, kot pa zrak.

Osvetlitev, ki prihaja iz okolice. S tem clenom upostevamo svetlobo, ki prihaja iz drugih teles, a jo ni mozno dolociti z zrcalnim odbojem svetlobe, ki prihaja od drugih teles. To je torej difuzni clen, ki manjka pri obravnavanju svetlobe, ki prihaja iz drugih teles, vendar iz neznane smeri.

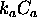
Cleni z vsotami torej predstavljajo svetlobo vec svetlobnih izvorov. Ostali cleni zajemajo svetlobo, ki je prisla na povrsino iz drugih povrsin ali iz okolice (zadnji clen). Konstante so zaradi upostevanja prehoda med seboj odvisne:

Vse konstante morajo biti tudi v ustreznih mejah 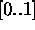. Barva C se v modelih obicajno izrazi kot

kjer je 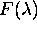funkcija odboja ali prehoda v odvisnosti od valovne dolzine 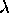; 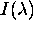pa je intenziteta vpadne svetlobe. Za zrcalni odboj 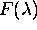ustreza Fresnelovi funkciji odboja. Za funkcijo prehoda lahko zapisemo podobno odvisnost kot pri konstantah

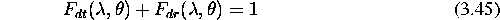
Hallov model lahko tudi izboljsamo, ce direktno uporabimo model Cook-Torrance pri odboju svetlobe izvorov, namesto kontrole obmocja odbleskov s Phongovim modelom. Dodatne izboljsave so mozne z vpeljavo intenzitete okolic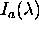e v izraze za difuzni prenos svetlobe.