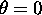 ima vrednost odbojnostne krivulje
ima vrednost odbojnostne krivulje
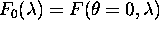 . Intenziteta odbite svetlobe
pri valovni dolzini
. Intenziteta odbite svetlobe
pri valovni dolzini 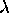 je enaka produktu intenzitete
vhodnega zarka pri tej valovni dolzini
je enaka produktu intenzitete
vhodnega zarka pri tej valovni dolzini 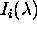 in
vrednosti Fresnelovega odboja
in
vrednosti Fresnelovega odboja 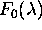 , kar lahko
zapisemo kot
, kar lahko
zapisemo kot
Dolocanje barve zrcalnega odboja je lahko zelo tezavno, ce moramo uporabiti tabelaricno podane vrednosti za odbojnost in jih uporabiti v Fresnelovih enacbah. Barva odbite svetlobe je odvisna od vpadnega kota na mikropovrsino in je za razliko od Phongovega modela, kjer je mozna uporaba le bele svetlobe, pri Cook-Torrance modelu odvisna tudi od barve svetlobnega izvora. Ce svetloba pade na povrsino pod pravim kotom, je barva odbite svetlobe enaka barvi materiala. Pri premikanju vpadnega zarka proti povrsini je barva odbite svetlobe vedno bolj podobna barvi vpadnega zarka. Izracun spremembo barve iz Fresnelovih enacb je lahko zamuden, zato je bolje, ce uporabimo ustrezno interpolacijsko shemo za izracun barve pri vmesnih kotih.
Pri pravokotni osvetlitvi vidimo barvo izvora pomnozeno s spektrom
odboja svetlobe objekta. Pri nizkih vpadnih kotih pa je videti odbito
barvo svetlobnega izbora skoraj nespremenjeno. Za izracun pri
vmesnih kotih lahko uporabimo linearno interpolacijo. Najprej pa je
potrebno dolociti barvo za oba ekstremna primera. Pravokotna
osvetlitev 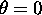 ima vrednost odbojnostne krivulje
ima vrednost odbojnostne krivulje
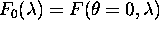 . Intenziteta odbite svetlobe
pri valovni dolzini
. Intenziteta odbite svetlobe
pri valovni dolzini 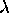 je enaka produktu intenzitete
vhodnega zarka pri tej valovni dolzini
je enaka produktu intenzitete
vhodnega zarka pri tej valovni dolzini 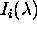 in
vrednosti Fresnelovega odboja
in
vrednosti Fresnelovega odboja 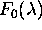 , kar lahko
zapisemo kot
, kar lahko
zapisemo kot
Pri kotu 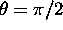 je vpadna svetloba vzporedna z
mikropovrsino. Fresnelov izraz pri tem kotu zapisemo kot
je vpadna svetloba vzporedna z
mikropovrsino. Fresnelov izraz pri tem kotu zapisemo kot
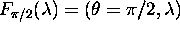 . Odbita svetloba ima
enako intenziteto kot vpadna svetloba, torej
. Odbita svetloba ima
enako intenziteto kot vpadna svetloba, torej
Odbojnost pri poljubnem kotu 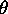 oznacimo kot
oznacimo kot
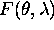 . Koncno lahko zapisemo intenziteto pri
valovni dolzini
. Koncno lahko zapisemo intenziteto pri
valovni dolzini  tako, da uporabimo mejne vrednosti barv
za dolocitev razpona in vrednosti Fresnelove funkcije pri izbranem
kotu za vmesne vrednosti. Pri standardni linerani interpolaciji
zapisemo enacbo kot
tako, da uporabimo mejne vrednosti barv
za dolocitev razpona in vrednosti Fresnelove funkcije pri izbranem
kotu za vmesne vrednosti. Pri standardni linerani interpolaciji
zapisemo enacbo kot
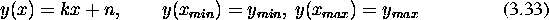
za katero lahko zapisemo ekvivalente pri barvni interpolaciji:
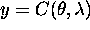
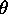
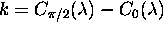
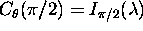 in pri pravokotni osvetlitvi
in pri pravokotni osvetlitvi
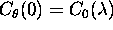
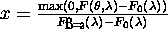
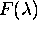 v meje
v meje 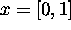
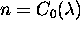
Pri izrazu za transformacijo x je potrebno uporabiti funkcijo 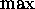 zaradi mozne numericne napake in negativnih vrednosti. S tem pa
zagotovimo pozitivnost tudi ob napaki in x v mejah. Intenziteto
lahko zapisemo kot
zaradi mozne numericne napake in negativnih vrednosti. S tem pa
zagotovimo pozitivnost tudi ob napaki in x v mejah. Intenziteto
lahko zapisemo kot
ali ce uporabimo osnovna izraza v enacbah (3.31) in (3.32)
kar kaze na to, da lahko izracunamo intenziteto odbitega
zarka pri zeljeni valovni dolzini in kotu 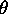 ze,
ce poznamo intenziteto vpadnega zarka
ze,
ce poznamo intenziteto vpadnega zarka 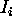 . Iz slik
2.2, 2.3 in 2.4, kot
tudi pripadajocih enacb, je razvidno, da je pri vpadnem kotu
. Iz slik
2.2, 2.3 in 2.4, kot
tudi pripadajocih enacb, je razvidno, da je pri vpadnem kotu
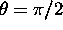 odbojnost vedno enaka ena. Zato lahko v enacbi
(3.35) uvedemo substitucijo
odbojnost vedno enaka ena. Zato lahko v enacbi
(3.35) uvedemo substitucijo
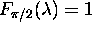 in s tem dobimo poenostavljeno enacbo
in s tem dobimo poenostavljeno enacbo
Za klasicni barvni model RGB lahko pri znanih komponentah
odbojnosti pod pravim kotom 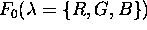 in
intenziteti vpadnega zarka
in
intenziteti vpadnega zarka 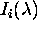 zapisemo
zapisemo
Racunska zahtevnost enacb (3.37) je le v
izracunavanju Fresnelove funkcije 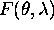 . Z
ustreznim tabeliranjem celotnih izrazov (3.37) in
(3.21), je mozna hitra dolocitev intenzitete
odboja za izbrani material. Z nekaj vec spomina je
mozno vpeljati model, ki bolje opisuje razmere, kot je
to primer pri Phongovem modelu, primernemu predvsem za opis
povrsin plastike. Kovine kazejo le majhno primes
difuznega odboja in imajo spreminjajoco barvo pri spreminjanju
vpadnega kota.
. Z
ustreznim tabeliranjem celotnih izrazov (3.37) in
(3.21), je mozna hitra dolocitev intenzitete
odboja za izbrani material. Z nekaj vec spomina je
mozno vpeljati model, ki bolje opisuje razmere, kot je
to primer pri Phongovem modelu, primernemu predvsem za opis
povrsin plastike. Kovine kazejo le majhno primes
difuznega odboja in imajo spreminjajoco barvo pri spreminjanju
vpadnega kota.