2.3.2 Fresnelove enacbe

Fresnelove enacbe temeljijo na fizikalnem opticnem modelu, saj obravnavajo polarizacijo svetlobe na gladki povrsini. Prevodniki ali kovine so opisani z lomnim kolicnikom, sposobnostjo odboja ( reflektanca) in indeksom izgub , ki je merilo za zmanjsanje intenzitete svetlobe na enoto dolzine. Indeks izgub je za dielektrike po definiciji enak nic.

Svetlobo, ki pod dolocenim kotom 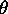pada na povrsino, lahko razdelimo na dve med seboj pravokotni ravnini valovanja elektricnega in magnetnega polja. Naravna nepolarizirana svetloba je zmes polariziranih valovanj v vseh smereh. Vsako valovanje pa lahko razdelimo na valovanje v dve med seboj pravokotni komponenti 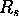in 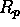. Odbojnost nepolarizirane svetlobe je povprecje 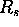in .

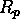Ce uporabimo enacbo (2.2) in (2.6), ter indeks izgub , lahko zapisemo enacbi odboja za polarizacijski ravnini na stiku med snovjo vpadnega zarka z lomnim kolicnikom 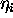in snovjo z lomnim kolicnikom 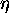, kot

kjer je vpadni kot glede na normalo; a in b pa sta dana kot

 

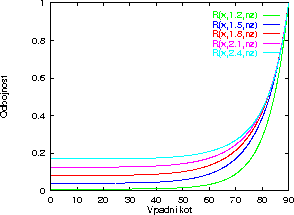
Za obravnavanje razmer pri stiku povrsin, kjer sta obe snovi dielektrika, lahko postavimo na nic in 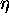uporabimo kot lomni kolicnik za drugi dielektrik. Pomembna razlika v odbojnosti pri dveh dielektrikih je razmerje med lomnim kolicnikom vstopne in izstopne snovi, kar lahko vidimo na sliki 2.2 in 2.3.

 

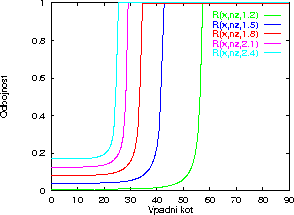
Iz navedenih slik lahko spoznamo dve pomembni lastnosti Fresnelovih enacb. Ko gre kot 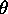proti 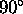(takrat je vpadni zarek vzporeden sticni ravnini), je odbojnost za vse snovi enaka ena.

Druga pomembna lastnost enacb je, da veljajo za vse vpadne kote 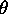. Za posebni primer, kjer je vpadni kot nic (zarek pravokotno na povrsino) in kjer je prva snov zrak (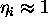), se lahko enacba (2.6) z uporabo Snellovega zakona (2.2), krajsa na obliko

Iz tega tudi sledi, da je odbojnost za steklo, ki ima tipicno vrednost lomnega kolicnika 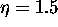, enaka

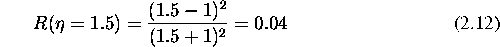
Razmerje 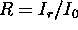med odbito svetlobo 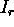in vpadno svetlobo 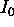je torej pri steklu, pri pravokotnem gledanju na povrsino, priblizno 4%. Zato se pri gladkih povrsinah normalno tudi vidi odblesk, ker vedno obstaja del svetlobe, ki se zrcalno odbije.

Iz slike 2.3 je pri prehodu iz snovi z visjim lomnim kolicnikom v snov z nizjim (zrak) opaziti posebno lastnost, kjer se pri dolocenemu kotu vpadni zarek pricne popolnoma odbijati. Zarek se pri tem giblje v notranjosti dielektrika ne da bi utrpel vecje izgube. Ta fenomen se imenuje popolni notranji odboj.

Ker lahko svetloba pri popolnem notranjem odboju potuje znotraj prozornega dielektrika skoraj brez izgub, je ta lastnost nasla uporabo pri prenosu informacij v opticnih kablih.

Lomni kolicnik 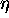je za dielektrike odvisen tudi od valovne dolzine. To je opaziti na prizmi, ki razprsi belo svetlobo v spekter barv. Pri kovinah pa je poleg lomnega kolicnika, od valovne dolzine odvisen tudi indeks izgub . V prevodnikih je potrebno obravnavati lomni kolicnik kot kompleksno velicino, ki je definirana kot

Podrobnejse podatke o konstantah za vecino materialov lahko najdemo v [Pal85]. Koeficienti se za geometrijski model dolocajo eksperimentalno tako, da se obravnava posamezne primarne barve (rdeca, zelena, modra) posamicno. Iz tega sledi, da imamo locene tudi lomne kolicnike 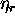, , 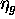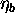. Iz enacbe (2.11) lahko izrazimo lomni kolicnik kot

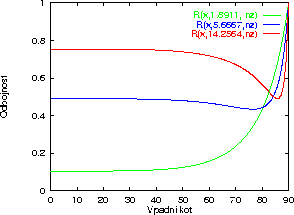
kar nam omogoca, da lahko dokaj enostavno izmerimo lomne kolicnike za posamezne primarne barve. Za glajen baker so koeficienti odboja R in lomni kolicniki 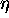primarnih barv podani v tabeli 2.2 (glej A. Watt [Wat90, strani 74-78,]).

Potek jakosti odboja posameznih primarnih barv za glajen baker in 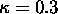je podan na sliki 2.4.

10mm