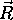Na sliki 4.3 sta prikazana tudi prispevka svetlobe z indirektno osvetlitvijo. Posamezen prispevek je odvisen od lastnosti povrsine. Gladke povrsine imajo visoko stopnjo odbojnosti, zato je mozno, da bo svetloba, ki prihaja od drugih povrsin opazno prispevala k skupni osvetlitvi v tocki. Podobno lahko trdimo tudi za prozorne povrsine. Mozne so tudi kombinacije obeh lastnosti. V preseku generiramo sekundarne zarke za odbite in prepuscene zarke, vendar le, ce ima povrsina take lastnosti, da je generiranje smiselno.
V smeri zrcalnega odboja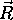 
je moc pricakovati
indirektno osvetlitev z najvecjo intenziteto. Ob znani normali v
preseciscu lahko smer odbitega zarka izrazimo kot
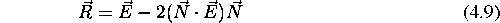
Pri dolocaju lomljenega zarka lahko uporabimo delni rezultat
iz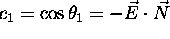 
. Obstaja vec metod
za dolocitev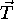 
, ki se razlikujejo po stevilu
operacij[Hec91]. Katera metoda je hitrejsa, je
odvisno od hitrosti osnovnih operacij ciljnega racunalnika, kot so
mnozenje, deljenje, sestevanje, ... Smer lomljenega zarka
po Heckbertovi metodi, ki je najenostavnejsa, dolocimo kot:
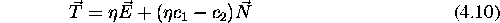
kjer je
in lomni kolicnik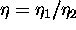 
. Vektorji morajo biti
normirani. Popolni notranji odboj na povrsini se zgodi, ko je
rezultat enacbe (4.11) imaginarno stevilo -- negativen
izraz pod korenom.
