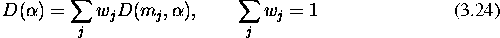


Next: 3.2.2 Geometrijski faktor slabljenja
Up: 3.2 Cook-Torrance model
Previous: 3.2 Cook-Torrance model
Vsebina: 
Zaradi razlicne orientacije mikropovrsin se tudi svetloba
odbija v razlicne smeri. Intenziteta svetlobe v doloceni smeri
je odvisna od stevila mikropovrsin orientiranih tako, da je
zrcalni odboj najvecji. Podobno kot v Phongovem modelu lahko tudi
tu uporabimo vektor 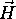 (3.16) kot merilo odboja v
doloceni smeri. Izraz
(3.16) kot merilo odboja v
doloceni smeri. Izraz 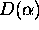 je porazdelitvena funkcija
intenzitete zrcalnega odboja v odvisnosti od kota
je porazdelitvena funkcija
intenzitete zrcalnega odboja v odvisnosti od kota 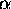 , ki je kot
med vektorjema
, ki je kot
med vektorjema 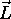 in
in 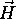 . Za porazdelitveno funkcijo bi
lahko uporabili razlicne funkcije, vendar se izkaze, da
Gaussova porazdelitvena funkcija dovolj dobro opisuje realne razmere.
. Za porazdelitveno funkcijo bi
lahko uporabili razlicne funkcije, vendar se izkaze, da
Gaussova porazdelitvena funkcija dovolj dobro opisuje realne razmere.
Sirino porazdelitvene funkcije kontroliramo s konstanto m, ki
predstavlja povprecni (RMS) nagib mikropovrsin. S
spreminjanjem m tako kontroliramo hrapavost povrsine. Z malimi
vrednostmi (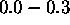 ) predstavljamo gladke, z vecjimi (
) predstavljamo gladke, z vecjimi (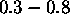 ) pa hrapave povrsine. Uporabna formula, za izracun D je
) pa hrapave povrsine. Uporabna formula, za izracun D je
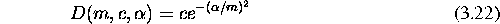
kjer je
c poljubna konstanta
e Eulerjeva konstanta.
Za bolj realen opis in s tem tudi racunsko zahtevnejsi opis
lahko uporabimo Beckmannovo porazdelitveno funkcijo:
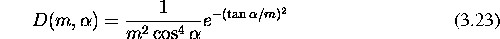
Prednost uporabe je poleg tocnosti tudi v tem, da enacba
(3.23) ne vsebuje konstante c, ki bi jo moral uporabnik
dolociti. Na sliki 3.9 sta primerjalno prikazani
obe porazdelitveni funkciji (3.22 in 3.23) iz
katerih je razvidno, da je Beckmannova porazdelitev sirsa in
nekoliko nizja od Gaussove, ce izberemo konstanto 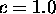 .
.
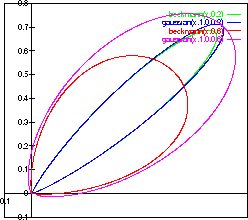
Slika 3.9: Gaussova in Beckmannova porazdelitvena funkcija 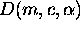 za
za 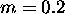 in
in 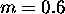 predstavljena s polarnim diagramom in
vektorjem odboja
predstavljena s polarnim diagramom in
vektorjem odboja 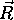 pod kotom
pod kotom 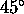
Izracun porazdelitvene enacbe lahko pospesimo tako, da
uporabimo interpolacijsko tabelo v odvisnost od kota 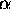 in
uporabljenih povrsin podanih s hrapavostjo m. Poleg osnovne
porazdelitve, lahko uporabimo tudi linearno kombinacijo razlicnih
tipov povrsin in s tem dobimo vecje moznosti za
popolnejsi opis, kar zapisemo kot uteznostno vsoto
porazdelitvenih funkcij:
in
uporabljenih povrsin podanih s hrapavostjo m. Poleg osnovne
porazdelitve, lahko uporabimo tudi linearno kombinacijo razlicnih
tipov povrsin in s tem dobimo vecje moznosti za
popolnejsi opis, kar zapisemo kot uteznostno vsoto
porazdelitvenih funkcij:
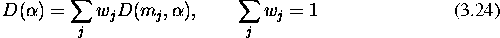
Copyright © 1995 Leon Kos, Univerza v Ljubljani
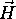 (3.16) kot merilo odboja v
doloceni smeri. Izraz
(3.16) kot merilo odboja v
doloceni smeri. Izraz 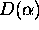 je porazdelitvena funkcija
intenzitete zrcalnega odboja v odvisnosti od kota
je porazdelitvena funkcija
intenzitete zrcalnega odboja v odvisnosti od kota 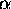 , ki je kot
med vektorjema
, ki je kot
med vektorjema 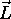 in
in 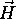 . Za porazdelitveno funkcijo bi
lahko uporabili razlicne funkcije, vendar se izkaze, da
Gaussova porazdelitvena funkcija dovolj dobro opisuje realne razmere.
. Za porazdelitveno funkcijo bi
lahko uporabili razlicne funkcije, vendar se izkaze, da
Gaussova porazdelitvena funkcija dovolj dobro opisuje realne razmere.
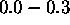 ) predstavljamo gladke, z vecjimi (
) predstavljamo gladke, z vecjimi (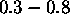 ) pa hrapave povrsine. Uporabna formula, za izracun D je
) pa hrapave povrsine. Uporabna formula, za izracun D je
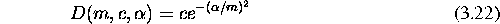
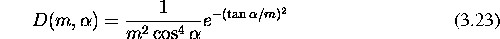
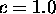 .
.

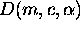 za
za 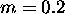 in
in 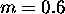 predstavljena s polarnim diagramom in
vektorjem odboja
predstavljena s polarnim diagramom in
vektorjem odboja 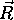 pod kotom
pod kotom 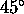
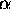 in
uporabljenih povrsin podanih s hrapavostjo m. Poleg osnovne
porazdelitve, lahko uporabimo tudi linearno kombinacijo razlicnih
tipov povrsin in s tem dobimo vecje moznosti za
popolnejsi opis, kar zapisemo kot uteznostno vsoto
porazdelitvenih funkcij:
in
uporabljenih povrsin podanih s hrapavostjo m. Poleg osnovne
porazdelitve, lahko uporabimo tudi linearno kombinacijo razlicnih
tipov povrsin in s tem dobimo vecje moznosti za
popolnejsi opis, kar zapisemo kot uteznostno vsoto
porazdelitvenih funkcij: