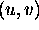Poleg predstavljenih osnovnih primitivov, se v racunalniski grafiki uporablja se mnozica raznoraznih povrsin s specificnimi lastnostmi. Primernost posameznih primitivov je odvisna od namena in zahtevnosti teorije, ki jo zelimo aplicirati.
Logicna razsititev trikotnikov na mnogokotnike je tudi ta, da mnogotnike sestavimo iz trikotnikov. Delaunay triangulacija[Mul94] je ena od uspesnih metod za planarne mnogokotnike poljubnih oblik. Razdelitev na mnozico trikotnikov pa nujno poveca racunski cas. Druge metode testiranja tocke v mnogokotniku so prikazane v [Hai94]. Hitrost testiranja notranjosti je poleg stevila vozlisc odvisna tudi od konveksnosti mnogokotnika.
Kvadriki (quadrics) so implicitne povrsine druge stopnje, za katere obstaja analiticna resitev presekov. Z variacijo parametrov v enacbi dobimo elipsoide, cilindre, svitke in druge objekte. Razsiritev z vecjim naborom osnovnih primitivov (kvadri, krogle, stozci) je mozna z uporabo superkvadrikov[Bar81] za katere obstaja analiticen test preseka z zarkom, vendar je potrebno presek izracunati numericno.
Splosna metoda pri resevanju parametricnih povrsin je
diskretizacija na stirikotnike in kasnejse inkrementalno
sencenje. Tak nacin seveda ni natancen. Pri grobih
delitvah takih povrsin so opazni Mach-ovi pasovi. Tocnejse
obravnavanje v veliki vecini zahteva numericno dolocanje
lokalnih koordinat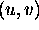 
. Numericno resevanje presekov pa
ima lahko tezave s singularnostjo zaradi raznih vzrokov.
V uporabi najdemo tudi druge implicitne, eksplicitne, algebraicne in proceduralne povrsine. Naj jih le nastejem: