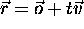 in
kroglo S definirano s centrom v tocki
in
kroglo S definirano s centrom v tocki 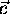 in radijem R.
Enacba povrsine na krogli je:
in radijem R.
Enacba povrsine na krogli je:
Krogle, kot enostavne in zaprte povrsine, so bile tudi najprej uporabljene v metodi sledenja zarku. Uporabljajo se tudi za omejitvene prostore (bounding volumes) kompliciranih objektov v algoritmih z vnaprejsnjim izlocanjem moznih presecnih objektov.
Predpostavimo, da imamo zarek 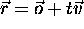 in
kroglo S definirano s centrom v tocki
in
kroglo S definirano s centrom v tocki 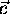 in radijem R.
Enacba povrsine na krogli je:
in radijem R.
Enacba povrsine na krogli je:
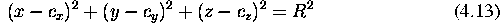
kar lahko zapisemo tudi v vektorski obliki za tocko 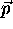 na povrsini:
na povrsini:
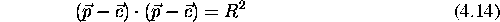
Zarek 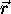 bo prebodel kroglo S pri vsaki vrednosti t, ki
zadovoljuje enacbo
bo prebodel kroglo S pri vsaki vrednosti t, ki
zadovoljuje enacbo
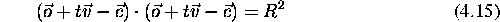
Z razsiritvijo dobimo kvadratno enacbo za parameter t:
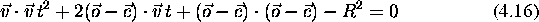
Resitev kvadratne enacbe nam da
Diskriminanta (izraz pod korenom) ogotavlja ali preseka
obstajata. Ce je pozitivna dobimo dva
presecisca. Ce je izraz nic se zarek le dotika
krogle. Pri negativnem izrazu pa presek zarka in krogle ne
obstaja. Smerni vektor 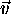 je lahko tudi enotski. Tedaj velja
je lahko tudi enotski. Tedaj velja
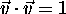 , kar dodatno poenostavi enacbo
(4.17). Z uvedbo enotskega vektorja je lahko t tudi
merilo za oddaljenost presecisca od izhodisca
, kar dodatno poenostavi enacbo
(4.17). Z uvedbo enotskega vektorja je lahko t tudi
merilo za oddaljenost presecisca od izhodisca
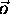 .
.