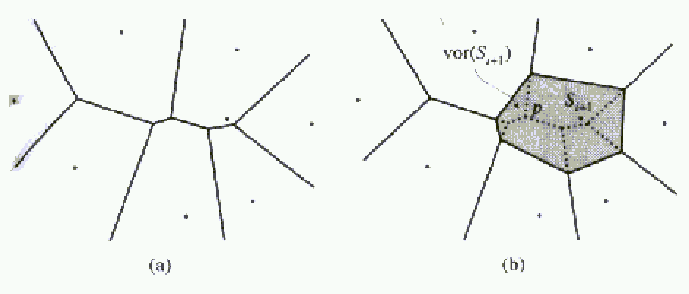
Figure 7: (a)
Obstaja vec nacinov konstrukcije Vornoi diagramov, ki se locijo po hitrosti in zahtevnosti algoritma. Najpreprostejsi nacin je inkrementalni algoritem.
Inkrementalni algoritem za konstrukcijo Vornoi diagrama temelji na postopnem dodajanju leg po nakljucnem vrstnem redu; podobno kot ze opisani inkrementalni algoritmi. Naj bo N niz leg na ravnini in G(N) Vornoi diagram, ki ga te lege dolocajo. Naj bo Ni niz prvih i nakljucno izbranih leg. Na vsaki stopnji i algoritem doloci Vornoi diagram G(Ni). Diagram G(Ni+1) nastane iz G(N) kot je prikazano na sliki 7

Figure 7: (a) ![]() ; (b)
; (b) ![]() ; (b) obmocje
; (b) obmocje ![]()
Naj bo ![]() i+1 lega, ki je dodana nakljucno. Najprej je
potrebno poiskati tocko p v
i+1 lega, ki je dodana nakljucno. Najprej je
potrebno poiskati tocko p v ![]() , ki lezi v Vornoi
obmocju tocke S. V tem primeru je S blizja tocki p kot
katerikoli drugi sosednji legi v
, ki lezi v Vornoi
obmocju tocke S. V tem primeru je S blizja tocki p kot
katerikoli drugi sosednji legi v ![]() .
.
Jasno je, da v diagramu
![]() tocka p ne bo vec njegov del. V vsakem trenutku
dodajanja i+1 je moznih vec tock p, vendar zadostuje ena
sama, ki je izbrana nakljucno. Ostale tocke (temena Vornoi
diagrama), ki so v obmocju S, je moc poiskati v diagramu
tocka p ne bo vec njegov del. V vsakem trenutku
dodajanja i+1 je moznih vec tock p, vendar zadostuje ena
sama, ki je izbrana nakljucno. Ostale tocke (temena Vornoi
diagrama), ki so v obmocju S, je moc poiskati v diagramu
![]() . Iskanje se zacne v tocki p in je preprosto
izvedljivo, saj so sosednja temena med seboj povezana z Vornoi robovi.
Robovi, ki so temenom p sosednji, se skrajsajo ali odstranijo.
Ce ima Vornoi rob obe krajisci v tockah p, se odstrani,
. Iskanje se zacne v tocki p in je preprosto
izvedljivo, saj so sosednja temena med seboj povezana z Vornoi robovi.
Robovi, ki so temenom p sosednji, se skrajsajo ali odstranijo.
Ce ima Vornoi rob obe krajisci v tockah p, se odstrani,
Ce je tocka p samo eno krajisce, se rob skrajsa.
Na koncu je potrebno dolociti se robove Vornoi obmocja
dodane lege S. Ti robovi povezujejo med seboj krajisca
odrezanih robov v kroznem vrstnem redu. Mesta, kjer se robovi
odrezejo, so dolocljiva z razpolavljanjem povezav med lego S
in ostalimi sosednjimi legami. Tako dobljen diagram je ![]() ).
).