Odnos med Delaunay-evo triangulacijo in Vornoi diagramom

Za razumevanje obeh pomembnih struktur D(P) in V(P) je potrebno poznati odnos med njima. Naj bo P nespremenljiv niz leg. Za Delaunay-evo triangulacijo veljajo lastnosti:

D1

D(P) je ravnocrtna dualnost V(P), po definiciji.

D2

D(P) je triangulacija, ce ne obstajajo stiri centricne lege: vsaka povrsina je trikotnik. Ploskve D(P) so Delaunay-evi trikotniki.

D3

Vsak trikotnik grafa D(P) ustreza temenu grafa V(P).

D4

Vsak rob grafa D(P) ustreza robu grafa V(P).

D5

Vsak vozel grafa D(P) ustrez obmocju grafa V(P).

D6

Meja D(P) je konveksna lupina

D7

Notranjost trikotnikov D(P) ne vsebuje nobenih leg.

Za Vornoi diagram veljajo naslednje lastnosti:

V1

Vsako Vornoi obmocje 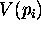je konveksno.

V2

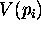je neomejeno, ce je pi na konveksni lupini niza leg.

V3

Ce je Vornoi teme na sticiscu 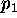V(), V(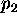) in V(p3), potem je v srediscu kroga C(v), ki ga dolocajo 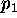, 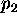in p3.

V4

C(v) je ocrtan krog pri Delaunay-evi triangulaciji, ki ustreza v.

V5

V notranjosti C(v) ni nobene lege.

V6

Ce je pj najblizji 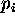, potem je 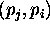rob triagulacije D(P).

V7

Ce obstaja krog skozi pi in pj, ki ne vsebuje nobenih drugih leg, potem je 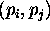rob triangulacije D(P).