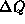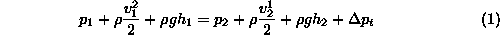
V primeru projektiranja nove fluidovodne mreze se hidravlicni preracun sestoji v glavnem iz dolocevanja potrebnih prerezov cevi in pritiska na mestih napajanja mreze ob upostevanju pogoja, da skozi posamezne cevi tece dolocena kolicina fluida potrebnega pritiska.
Lahko pa naletimo tudi na drugo vrsto naloge in sicer, da so doloceni posamezni premeri cevi in dotoki oz. odtoki iz mreze, nasa naloga pa je dolociti stanje v mrezi, to pomeni dolociti pretoke v ceveh in tlake v posameznih vozliscih. Potrebno je torej narediti analizo dogajanja v mrezi.
Osnovna enacba hidrodinamike je seveda Bernoulijeva enacba za stacionarni tok nestisljivega fluida za sistem s trenjem 153
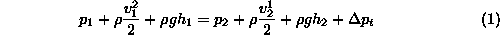
Ker se prerez v cevi ne spreminja je hitrost fluida konstantna, tako lahko napisemo enacbo za tlak na izhodu

V ceveh se lahko pojavlja laminarni ali turbulenten tok 154
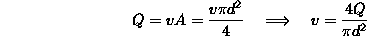
katerega razmejuje Reynoldsovo stevilo 156

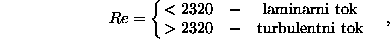
kjer je Q pretok v cevi premera d in  kinematicna viskoznost
fluida (voda pri 293K :
kinematicna viskoznost
fluida (voda pri 293K : 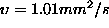 ).
).
Ne glede na to pred kaksno nalogo stojimo in s kaksnim tipom mreze imamo opravka, morata biti izpolnjena sledeca dva zakona hidravlike:
Podobno lahko vzamemo celotno omrezje kot eno vozlisce, zato mora biti vsota vseh dotokov in odtokov prav tako enaka nic. Ce to ne bi bilo tako, bi najverjetneje omrezje nekje puscalo.
Izgubo tlaka zaradi odpora pri toku fluida z gostoto 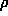 in
hitrostjo v izracunamo z enacbo
in
hitrostjo v izracunamo z enacbo

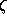 je koeficient izgub, ki je pri ravnih ceveh s kroznim
prerezom
je koeficient izgub, ki je pri ravnih ceveh s kroznim
prerezom

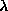 je koeficient trenja, l je dolzina cevi, d je premer cevi.
je koeficient trenja, l je dolzina cevi, d je premer cevi.
Enacbo za izgubo (padec) tlaka v cevi lahko tako napisemo 157

Ce bi napisali sistem enacb za mrezo tokov, bi dobili nelinearni
sistem enacb saj je padec tlaka kvadraticno odvisen od pretoka
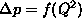 in s tem prakticno neresljiv.
Pomagamo si z linearizacijo enacb(4). V okolici delovne
tocke
in s tem prakticno neresljiv.
Pomagamo si z linearizacijo enacb(4). V okolici delovne
tocke 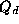 se nelinearna funkcija obnasa linearno.
Pretok lahko napisemo kot
se nelinearna funkcija obnasa linearno.
Pretok lahko napisemo kot
Funkcijo 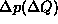 razvijemo v Taylorjevo vrsto z uporabo
enacbe 45
razvijemo v Taylorjevo vrsto z uporabo
enacbe 45
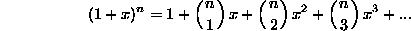
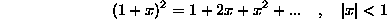
in upostevamo le linearni clen, saj naj bi bil neznan odmik 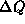 od fiksne delovne tocke majhen in s tem napaka pri linearizaciji
dovolj majhna.
od fiksne delovne tocke majhen in s tem napaka pri linearizaciji
dovolj majhna.
Drugace zapisana enacba (6) pokaze linearno
odvisnost padca tlaka 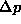 od male spremembe
od male spremembe