Naj bo 
niz tock na ravnini, ki se
imenujejo lege. Vornoi diagram V(p) ravnino razdeli tako, da je
sestavljen iz vseh tock, ki so vsaj tako blizu legi, kot so blizu
katerikoli drugi legi:
Naj bosta na ravnini samo dve legi, 
in .
Naj premica
pravokotno razdeli segment 
na dva enaka dela.
Potem je vsaka tocka x na premici 
enako oddaljena od
lege , kakor tudi od lege . Velja 
Ce lezijo na ravnini tri lege 
, te definirajo
trikotnik. Razpolovnice stranic trikotnika , 
in
se sekajo v tocki, ki je sredisce ocrtanega
kroga. Sredisce ni nujno v notranjosti trikotnika.
Iz prvih dveh primerov je razvidno, da imajo razpolovnice 
pomembno vlogo. Naj bo 
zaprta polravnina, ki je omejena z
in vsebuje tocko 
. Potem lahko razumemo kot vse
tocke, ki so blize pi kot pj. Kot ze omenjeno je 
niz
tock, ki so blize legi , kot katerikoli drugi legi: z
drugimi besedami, tocke blize kot , blize pi kot ,
blize pi kot p3, itd. Upostevaje navedeno je mogoce
napisati enacbo za Vornoi diagram :
pri cemer je potrebno upostevati presek preko vseh i in j,
za katere velja 
. Iz enacbe sledi lastnost Vornoi
diagrama: obmocja Vornoi diagrama so konveksna, ker nastanejo kot
presecisca vecih polravnin. Kadar so ta obmocja
omejena, so to konveksni mnogokotniki. Robovi se imenujejo Vornoi
robovi in temena Vornoi temena. Katerakoli tocka na Vornoi robu
ima dve najblizji legi, Vornoi teme pa ima najmanj tri
najblizje lege.
V primeru stirih leg na ravnini, ki oblikujejo vogale kvadrata, je Vornoi diagram kot je prikazano na 5a. Vornoi teme je v tem primeru cetrte stopnje. Ce se eno lego nekoliko premakne (Slika 5b), postane diagram normalen. Prvi primer je izrojen zaradi centricnega polozaja stirih leg.
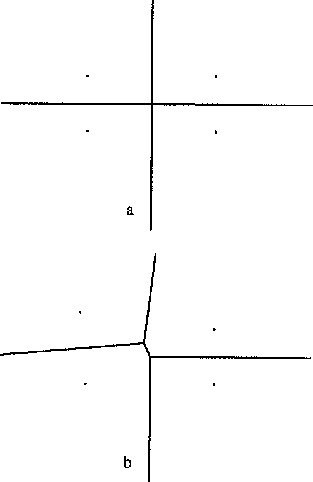
Figure 5: Vornoi diagram s stirimi tockami
