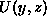 je mozna na vec nacinov. Iz enacbe
(4) je razvidno, da je potrebno izracunati prostornino, ki jo
ploskev U obdaja. Ker so nase osnovne ploskvice kvadrati si
izberemo bilinearno funkcijo, ki je krizni produkt dveh linearnih
funkcij
je mozna na vec nacinov. Iz enacbe
(4) je razvidno, da je potrebno izracunati prostornino, ki jo
ploskev U obdaja. Ker so nase osnovne ploskvice kvadrati si
izberemo bilinearno funkcijo, ki je krizni produkt dveh linearnih
funkcij
Integracija funkcije 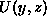 je mozna na vec nacinov. Iz enacbe
(4) je razvidno, da je potrebno izracunati prostornino, ki jo
ploskev U obdaja. Ker so nase osnovne ploskvice kvadrati si
izberemo bilinearno funkcijo, ki je krizni produkt dveh linearnih
funkcij
je mozna na vec nacinov. Iz enacbe
(4) je razvidno, da je potrebno izracunati prostornino, ki jo
ploskev U obdaja. Ker so nase osnovne ploskvice kvadrati si
izberemo bilinearno funkcijo, ki je krizni produkt dveh linearnih
funkcij
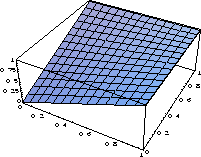
Za podane vrednosti 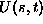 v robnih tockah lahko izracunamo
splosne koeficiente
v robnih tockah lahko izracunamo
splosne koeficiente 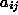 kot sistem linearnih enacb
kot sistem linearnih enacb
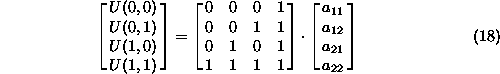
Matriko sistema invertiramo in napisemo enacbo
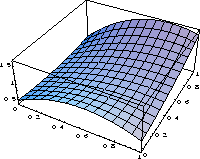
Za prakticen primer vzemimo funkcijo na sliki 5 s tockami
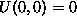 ,
, 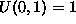 ,
, 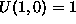 ,
, 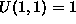 . Z izracunom enacbe
(19) dobimo koeficiente
. Z izracunom enacbe
(19) dobimo koeficiente 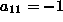 ,
,  ,
, 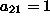 ,
,
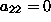 . Funkcija (17) je tako
. Funkcija (17) je tako
Ce zelimo izracunati prostornino, ki jo ploskev U obdaja integriramo enacbo (17)
Iz enacbe (21) lahko razberemo to, da znamo izracunati volumen, ki ga obdaja ploskev, ze ce poznamo vrednosti v ogliscih. Potrebno je le zmnoziti enacbe (19), kar je v primeru nase bilinerarne funkcije enostavno
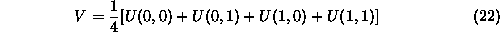
Torzijski vztrajnosti moment za primer mreze na sliki 2 po enacbi (4) je z uporabo bilinearne funkcije enak
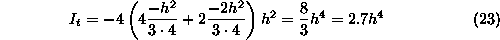
Iz literature [6] razberemo, da je za razmerje stranic 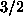 torzijski moment
torzijski moment 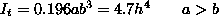 , kar nam
daje slutiti, da bo za vecje natancnosti potrebno zgostiti mrezo.
, kar nam
daje slutiti, da bo za vecje natancnosti potrebno zgostiti mrezo.
Seveda je natancneje, ce za interpolacijsko funkcjo izberemo ploskev visjega reda, ki se razteza preko vec tock. Podobno kot pri bilinerani funkciji naredimo krizni produkt dveh parabolicnih funkcij z istim razponom parametrov s in t.
ali zapisano v matricni obliki
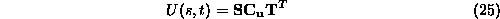
kjer so 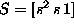 ,
, 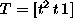 in
in
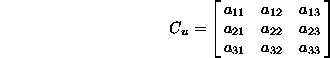
Podobno kot v prejsnem primeru je potrebno izracunati koeficiente
matrike 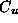 . Imamo devet tock
. Imamo devet tock 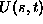 ; Zapisemo devet linearnih
enacb
; Zapisemo devet linearnih
enacb 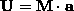

Sistem enacb 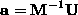 resimo z invertiranjem
matrike M
resimo z invertiranjem
matrike M
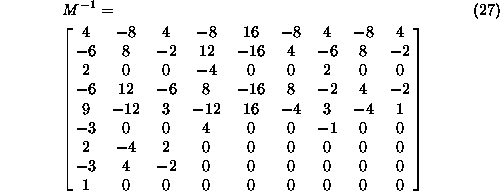
Prostornino, ki jo obdaja ploskev izracunamo z integriranjem enacbe (24)
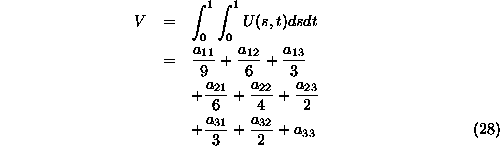
Za robne tocke 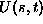 na sliki 6 lahko izracunamo
sledece koeficiente
na sliki 6 lahko izracunamo
sledece koeficiente 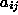 in z njimi prostornino
in z njimi prostornino 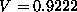

Pri aproksimaciji funkcije z bikvadraticno funkcijo je potrebno paziti, da lahko celotno podrocje, ki je sestavljeno iz osnovnih ploskvic, popisemo z osnovno ploskvico. To konkretno pomeni, da moramo imeti v obeh smereh sodo stevilo intervalov. V primeru na sliki 2 to ne velja, lahko pa si pomagamo tako, da vecino ploskvic izracunamo z bikvadraticno aproksimacijo, za preostale pa uporabimo bilinearno.