Univerza v Ljubljani

Fakulteta za strojnistvo

Laboratorij za CAD - LECAD

Metoda koncnih elementov

Povzetek studija

Tomaz Kolsek

Ljubljana, januar 1998

Kazalo vsebine :

UVOD 2

1 Teoreticne osnove 4

Poljska in interpolacijska matrika 5

Osnovna enacba koncnega elementa 5

Transformacijske matrike 6

enacba konstrukcije 7

Robni pogoji 9

Zunanja obremenitev 10

2 Tipi elementov in uporaba 11

Elementi za linijske konstrukcije 12

Elementi za ploskovne konstrukcije 13

Elementi za modeliranje teles 16

Osnosimetricne konstrukcije 16

Elementi za posebne namene 17

3 Posplositev metode koncnih elementov 18

Prenos toplote in termoelasticnost 19

Dinamika konstrukcij 19

Stabilnostni problemi 21

Problemi plastomehanike 22

4 Literatura 23

UVOD

Pri resevanju kompleksnih napetostno-deformacijskih problemov v strojnistvu vse vec uporabljamo numericne metode, saj je znano, da je z analiticnimi racunskimi metodami mogoce dolocevati le mocno poenostavljene konstrukcijske modele. Z razvojem zmogljivih racunalnikov je se posebno dobila na veljavi t.i. metoda koncnih elementov, katero je mogoce aplicirati na sirsa podrocja mehanike in fizike, kot so elastomehanika, prenos toplote, dinamika konstrukcij, stabilnost, hidromehanika, podrocja geomehanike, plastomehanika itd. Posebno pogosti problemi konstruiranja pa nastopajo zlasti na podrocju elastomehanike, kjer se je tudi najprej razvila. Metoda temelji na diskretizaciji poljubne konstrukcije na ustrezne koncne elemente in uporabi matricne algebre.

Za potrebe resevanja omenjenih problemov so se razvili racunalniski programi, ki uporabniku ob dolocenem inzenirskem predznanju omogocajo simulacijo dogajanja v konstrukcijah pod vplivom obremenitev. Med najbolj znanimi produkti so npr. MSC-NASTRAN, SDRC-IDEAS, ANSYS, ABAQUS, ... Naceloma poteka resevanje problema v naslednjih fazah:

- izdelava geometrijskega racunalniskega modela konstrukcije (3D modeliranje)

- diskretizacija (razdelitev modela na manjse delcke-koncne el. ustreznega tipa)

- definiranje robnih pogojev in obremenitev

- samodejni izracun zahtevanih kolicin (izracunavanje)

- prikaz rezultatov izracuna (postprocesiranje)

Uporabniku vzame najvec casa priprava oziroma nastavitev modela (preprocesiranje). V prvi fazi uporabnik definira geometrijo konstrukcije (modela), ki je sestavljena iz tock, robov, povrsin in volumnov dolocenih dimenzij. Nato se geometrijski model diskretizira (razdeli) z ustreznim tipom koncnih elementov. Na kvaliteto rezultatov bistveno vpliva ustreznost tipa elementov in njihova porazdelitev po konstrukciji (mreza elementov). Nadalje se definirajo se t.i. robni pogoji, ki v vecini primerov popisujejo vpetja konstrukcije, morebitne simetricnosti v konstrukciji ter povezavo s sosednjimi elementi sistema. Potem definiramo se razlicne vrste obremenitev, npr. vozliscne (koncentrirane, tockovne) sile, tlake (porazdelitev sile po vecjih ploskvah), vplive masnih sil (teza, transl. in rotacijski pospeski, centrifugalna sila) in vpliv temperature.

Tako pripravljene podatke program uredi v matricne zapise. Ob upostevanju znanih robnih pogojev (vpetij) se za elastomehanske probleme dobi kot rezultat mnozica vozliscnih pomikov. Matricne operacije so pri velikem stevilu elementov izredno obsezne, tako da se v tej fazi izkaze prednost racunalnikov s hitrimi procesorji in velikimi pomnilniki. Ce so rezultati analize obsezni, jih najraje prikazujemo graficno v obliki barvnih polj in diagramov. Na ta nacin je mogoce zelo hitro kvalitativno oceniti mesta na konstrukciji, kjer nastopajo koncentracije velicin, ki nas zanimajo.

1 Teoreticne osnove

Prikazali bomo, kako se resujejo problemi elastostatike, za zacetek pa imejmo opravka z linearnimi problemi. Znano je, da tovrstne probleme lahko opisemo z elementi napetostnega tenzorja _ij, deformacijskega tenzorja _ij in vektorja pomikov u_i. Teh 15 elementov elastostatike je povezanjih med seboj z

- ravnoteznimi enacbami sigma_ij,j + X_j = 0

- zveze med majhnimi spec. def. in pomiki eps_ij = ½(u_i,j + u_j,i)

- Hookovimi zakoni za majhne def. sigma_ij = 2µ_ij + lambda eps_kkdelta_ij - T(2µ+3 lambda)delta_ij

V slednjih enacbah smo upostevali tudi vpliv temperature. Kadar porazdelitve temperature po kontinuumu vnaprej ne poznamo, izracunamo to kolicino predhodno iz prenosne enacbe toplote:

k T_,ii + Q_i = rho C_E T .

Elastostaticni problem bo torej resen, cim izracunamo iz zgornjih enacb vse komponente sigma_ij, epsilon_ij in u_i. Ob tem je potrebno upostevati robne pogoje in zunanjo obremenitev

kontinuuma.

Robni pogoji so lahko npr. taksni, da so na povrsini predpisane sile

p_i = sigma_ij n_j

ali pomiki

u_i = f_i(x,y,z)

ali pa so predpisani mesani robni pogoji. Enacbe dajo enolicne resitve, le ce so izpolnjeni kompatibilnostni pogoji.

Pri MKE lahko uporabimo namesto ravnoteznih enacb bolj uporaben princip mehanike in sicer princip virtualnih pomikov, ki govori o enakosti virtualnega dela zunanjih in notranjih sil kontinuuma

mdelta W^z = mdelta Wⁿ oziroma

mdelta vdelta _i p_i = integral mdelta epsilon _ij sigma _ij dV

Nastete enacbe za MKE priredimo v matricno obliko, saj le-ta nudi celo vrsto prednosti pri racunalniskem programiranju. Tako ima vektor {sigma} 6 neodvisnih komponent, vektor {epsilon} 6 in vektor {u} 3 komponente. Matricni zapis ravnoteznih enacb bi torej bil

[d]^T{sigma} + {X} = {0} ,

kjer je [d] matrika diferencialnih operatorjev. Specificne deformacije so

{eps} = [d]{u}

in Hookov zakon

{sigma} = [E]{epsilon}+{sigma^temp} ,

kjer je [E] matrika elasticnih konstant.

1.1 Poljska in interpolacijska matrika

Ko razdelimo (diskretiziramo) konstrukcijo na koncne elemente, dobimo e elementov. Vsak element ima polje in vozlisca, elementi pa so le preko vozlisc povezani v prvotno celoto (slika 2).

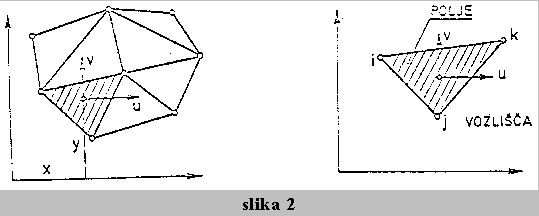Pomik tocke v polju elementa je v splosnem odvisen od koordinat. Ta zakon je v splosnem vnaprej neznan in ga pri MKE predpostavimo. Za poljuben koncni element lahko zapisemo enacbo za pomike v polju na naslednji nacin:

{u} = [a]{c}

V tej enacbi je [a] poljska matrika elementa, {c} pa je vektor konstant. Najenostavnejse poljske matrike dobimo, ce predpostavimo linearen zakon poteka pomikov v polju. Splosno pa je znano, da opisejo polinomi visjih redov boljse, t.j. natancnejse vrednosti pomikov po kontinuumu, vendar v teh primerih postanejo racunske operacije vse obseznejse. Tako bomo govorili o elementarnih (linearnih) in o visjih (parabolicnih, kubicnih) tipih koncnih elementov.

Izbor matrike [a] in {c} zavisi predvsem od izbire vozliscnih vektorjev elementov. Vektor vozliscnih pomikov {U} ima toliko komponent, kolikor prostostnih stopenj predpisemo elementu. Za posamezna vozlisca lahko npr. predpisemo pomike v dolocenih smereh, lahko pa tudi zasuke (tangente). Splosno torej lahko pisemo, da je za robne pogoje

{u^konturi} = {U} in [a] = [a^konturi] , torej

{U} = [a^konturi]{c}, torej {c} = [a^konturi]^-1 {U} .

Tako je z invertiranjem [a^k] mogoce dolociti {c}. Koncno lahko zapisemo

{u} = [a][a^k]^-1{U}

oziroma z novo simboliko

{u} = [b]{U}

Matriko [b] imenujemo interpolacijska matrika in je temeljnega pomena za MKE. Ko je ta funkcija izbrana, potekajo vse nadaljne racunske operacije po enotnem postopku.

1.2 Osnovna enacba koncnega elementa

Najprej si izracunamo specificne deformacije {epsilon} in napetosti {sigma} v odvisnosti od vozliscnega vektorja {U}. Tako je

{epsilon} = [d] [u] = [d] [b] {U} ali z novo simboliko

{epsilon} = [p] {U}

Podobno dobimo za napetosti

{sigma} = [E] {epsilon} + {sigma ^t} = [E] [p] {U} + {sigma ^t}

Enacbe povedo, da lahko dolocimo deformacije in napetosti v poljubni tocki elementa, ce le poznamo vozliscni vektor {U}. Da pa dolocimo ta vektor, pa nastavimo osnovno enacbo koncnega elementa. Pri tem si pomagamo s principom virtualnih pomikov. Ce z {F} oznacimo vozliscne sile elementa, smemo zapisati za virtualno delo zunanjih sil na elementu

mdelta W^z = {U}^T {F}

Virtualno delo notranjih sil pa je

mdelta Wⁿ = integral {mdelta epsilon}^T {sigma} dV

Ko vstavimo se enacbe za {epslon} in {sigma} , dobimo

mdelta Wⁿ = integral ([p]{mdelta U})^T([E][p]{U}+{sigma ^t}) dV

Z izenacevanjem zgornjih enacb dobimo za elasticne ravnotezne sisteme

{F} = integral [p]^T[E][p]dV {U} + integral [p]^T{sigma ^t}dV

Ce oznacimo integrala v enacbi s

[K] = integral [p]^T[E][p]dV in {F ^t} = integral [p]^T{^t}dV ,

dobimo osnovno enacbo koncnega elementa

{F} = [K] {U} + {F^t}

oziroma ce temperaturne obremenitve ne nastopajo

{F} = [K] {U}

Enacba podaja zvezo med vozliscnimi silami {F} in vozliscnimi pomiki elementa {U}. Togostno matriko [K] lahko izracunamo za vnaprej izbrani element. Ta matrika vsebuje le geometrijo elementa in fizikalne konstante materiala. Vcasih je primerneje, ce uporabimo t.i. posploseno (generalizirano) togostno matriko [K_q], ki je neodvisna od polozaja v prostoru, kjer iz [K] izlocimo vpliv polozaja [a^k]^-1 :

[K] = ([a^k]^-1)^T[K_q][a^k]^-1

Z ustreznim zdruzevanjem vseh enacb v t.i. enacbo konstrukcije pa bo mogoce ob upostevanju robnih pogojev celotne konstrukcije (podpore) in poznane zunanje obremenitve poiskati iz nastalega sistema linearnih enacb vse neznanke vektorja {U}.

1.3 Transformacijske matrike

Pogostoma lezijo elementi na konstrukciji poljubno v prostoru, zato je potrebno vse osnovne enacbe koncnih elementov izraziti v skupnem (globalnem) koordinatnem sistemu. To izvedemo s transformacijskimi matrikami. V splosnem transformiramo vektor {v} iz sistema) (x,y,z) v sistem (eta,ni,ceta) na naslednji nacin:

{v}_eta,ni,ceta = [T_o]{v}_x,y,z

S [T_o] oznacimo osnovno transformacijsko matriko in ima eksplicitni zapis

Pri MKE imamo opravka s posplosenimi vektorji, ki imajo obicajno veliko komponent. Transformiramo jih s posploseno transformacijsko matriko [T]

ce uvedemo nove oznacbe za vektorje in matrike v globalnem koordinatnem sistemu {F'} [K'] in {U'}, kjer se transformirajo

{F'} = [T] {F}

{U'} = [T] {U}

in [K'] = [T] [K] [T]^T ,

dobimo

{F'} = [K'] {U'}

Transformiranje togostne matrike iz lokalnega v globalni koordinatni sistem zahteva pri prakticnem racunanju veliko racunalniskega casa.

1.4 enacba konstrukcije

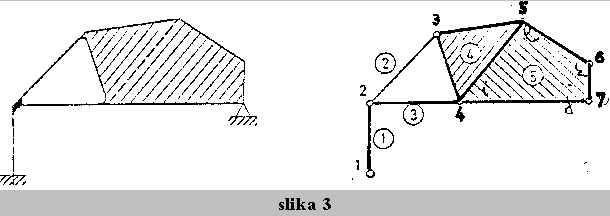
Enacba konstrukcije nastane tako, da zdruzimo vse enacbe koncnih elementov v skupno enacbo, ki jo zapisemo simbolicno

{F} = [K] {U}

V vektor {F} zdruzimo vse vozliscne sile {F_i}, v vektor {U} pa vse vozliscne pomike {U_i}. Togostna matrika [K] je simetricna in sestavljena iz n x n podmatrik [K_rs], ki nastanejo z zdruzevanjem parcialnih togostnih matrik posameznih elementov.

V praksi se pokaze, da je precej elementov togostne matrike enakih 0. Razvili so se algoritmi, ki ob ustreznem prestevilcenju vozlisc zozijo diagonalni pas v matriki, kjer nastopajo potencialno nenicni elementi. Tako prirejena togostna matrika nudi bistvene prihranke na casu racunanja ustreznih velicin pri MKE. Pri postopku racunanja neznanih velicin iz enacbe konstrukcije je namrec potrebno invertirati togostno matriko. Med najbolj pogosto uporabljanimi metodami je t.i. Lower-Upper dekompozicija, ki razstavi matriko na produkt dveh matrik, od katerih ima ena matrika nenicne elemente le na diagonali in pod njo (lower) ter druga na diagonali in nad njo (upper), invertiranje teh matrik pa je racunsko nezahtevno. Obstajajo tudi iterativne metode, ki v dolocenih pogojih hitreje pripeljejo do resitve, kot invertiranje matrik. Nasploh je izracunavanje sistema "know-how" proizvajalca programske opreme.

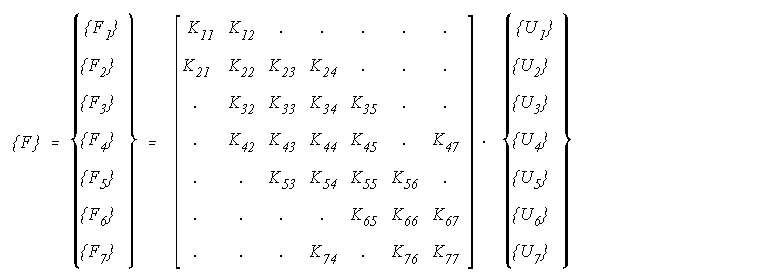1.5 Robni pogoji

Vsaka konstrukcija, ki jo obravnavamo pri statiki, mora biti stabilno podprta, zato je del vozliscnih pomikov (zasukov) znanih (predpisanih). Ti pomiki (zasuki, tangente,...) predstavljajo robne pogoje konstrukcije.

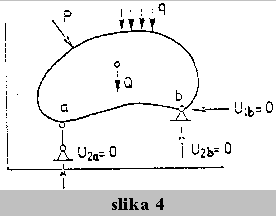S primerno preureditvijo enacbe konstrukcije-s parcioniranjem-lahko izracunamo najprej vse neznane komponente vektorja {U}, nato pa se nepoznane reakcije, t.j. nepoznane komponente vektorja {F}.

Ob poznavanju robnih pogojev {U}_r (obicajno nepodajne podpore, upostevanje simetrije konstrukcije,...) lahko dolocimo nepoznane pomike

{U}_m = [K]_mm^-1({F}_m-[K]_mr{U}_r)

Tako so doloceni vse komponente vozliscnih vektorjev {U}, nato pa je mogoce dolociti se reakcije {F}_r.

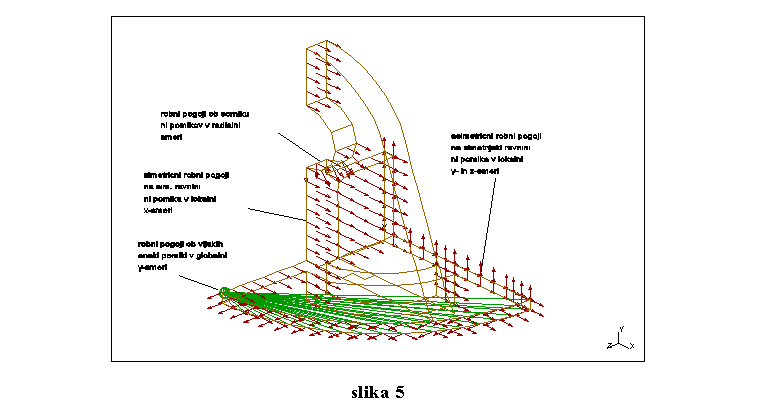
Za prakso so uporabni naslednji popisi robnih pogojev:

- nepodajne podpore

- upostevanje morebitnih simetricnosti v konstrukciji

- izlocanje dolocenega stevila prostostnih stopenj iz racuna

- medsebojna povezava pomikov dolocenih tock (simulacija ciklicne simetrije)

1.6 Zunanja obremenitev

Sile, ki obremenjujejo konstrukcijo, delujejo na diskretizirani model le preko vozlisc. Zato je ze pri pripravi modela potrebno upostevati obremenitev tako, da izberemo vozlisca elementov tam, kjer sile nastopajo. Pri porazdeljeni obremenitvi pa moramo nadomestiti obremenitev polja ali roba elementa z ekvivalentnimi vozliscnimi komponentami. Za splosne primere dosezemo to ekvivalenco z uporabo principa virtualnih pomikov.

mdelta W ^vozlisca = mdelta W ^polja .

Ce z {q} oznacimo vektor obremenitve na enoto ploskve elementa in z {u} tem obremenitvam prirejene virtualne pomike, potem lahko pisemo

mdelta W ^polja = integral {mdelta u}^T{q} dA = { mdelta U}^T integral [b]^T{q} dA

Vektor ekvivalentnih sil pa je

{F ^ek} = integral [b]^T{q} dA

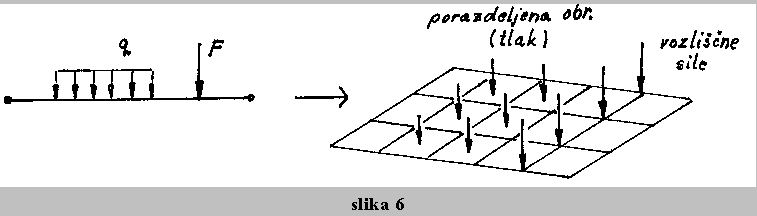V praksi omogocajo programi za pripravo podatkov razlicne nacine podajanja obremenitev, programska oprema pa samodejno poskrbi za ustrezno interpolacijo na vozlisca. Tako npr. lahko enostavno definiramo:

- tockovne obremenitve na vozliscih

- povrsinske obremenitve na ploskvah elementov

- tlake na robovih

- definiranje obremenitev na geometriji namesto na mrezi elementov in vozlisc (je bolj intuitivno)

- podajanje obremenitev in robnih pogojev s pomocjo variabilnih podatkovnih 3D polj, ki so definirana na geometriji, vrednosti v posameznih tockah pa so podane npr. z meritvami ali algebraicnimi funkcijami.

2 Tipi elementov in uporaba

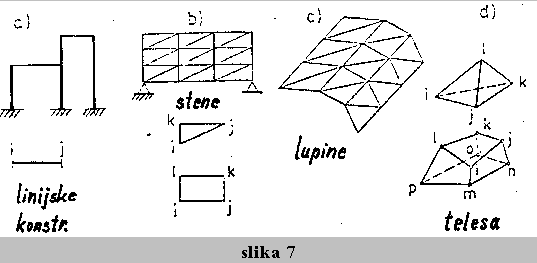
Konstrukcijo lahko glede na sestavne elemente (nosilci, plosce,...) razvrstimo v dolocene tipe konstrukcije, npr. linijske, ploskovne in konstrukcije z izrazenim volumnom. Pri uporabi MKE lahko dele konstrukcij ponazorimo z uporabo razlicnih vrst elementov, ki jih preko vozlisc povezemo v celoto. Zato obstaja cela vrsta razlicnih elementov, ki s svojimi lastnostmi simulirajo obnasanje konstrukcije pod vplivom obremenitev. Tako se je razvilo vec tipov linijskih elementov za ponazoritev nosilcev, elementov za modeliranje sten, plosc, lupin in teles. Posamezni tipi elementov se razlikujejo glede na obliko, stevilo vozlisc, interpolacijske funkcije, stevilo prostostnih stopenj v vozliscih, ... Od presoje inzenirja je odvisno, kaksen tip elementa bo uporabil za modeliranje posameznega dela konstrukcije. Od poznavanja lastnosti uporabljenih elementov je odvisna tudi interpretacija rezultatov, ki jih daje MKE.

2.1 Elementi za linijske konstrukcije

Najprej se je MKE uveljavila na podrocju linijskih konstrukcij. Izbor tipa elementa pogojuje obliko togostne matrike elementa. Tako ima npr. togostna matrika linijskega elementa (slika 8) v prostoru z 12 prostostnimi stopnjami (3 pomiki in 3 zasuki v obeh vozliscih) 12 x 12 elementov, ki so funkcije staticnih velicin E, A, I, s (material, prerez, vztrajnostni moment, dolzina). Za ravninsko konstrukcijo padejo cleni, ki vsebujejo vpliv momenta M_x in M_y, matrika [K] pa je ranga 6 x 6. Za palicje odpadejo nadalje se cleni z vplivom preostalih momentov in togostna matrika se se bolj poenostavi.

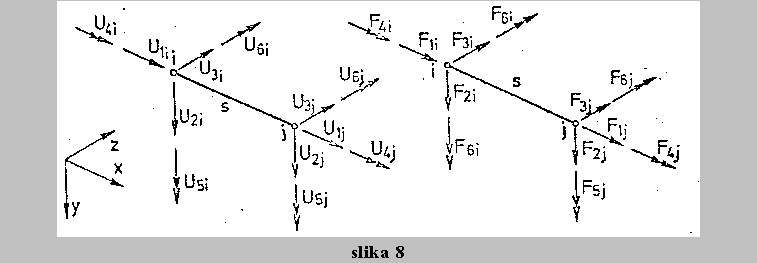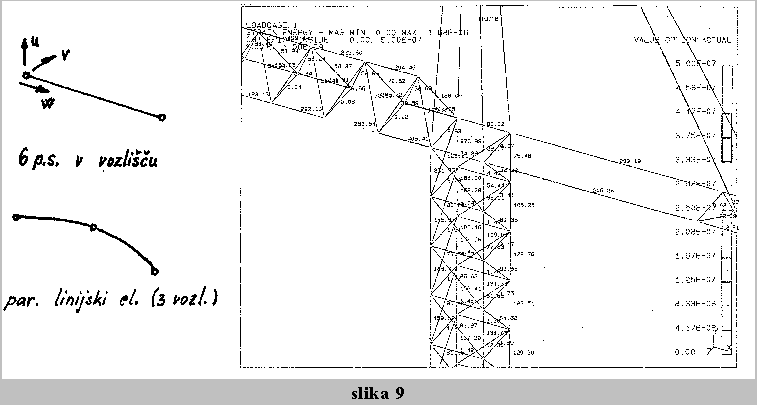
Programska oprema nudi uporabniku obicajno linearne in parabolicne linijske elemente z dvema oziroma tremi vozlisci.

Prerez je lahko poljuben in ga definira uporabnik, obstajajo pa ze izdelane knjiznice standardnih prerezov (I-profili, okrogli, skatlasti in drugi preseki).

2.2 Elementi za ploskovne konstrukcije

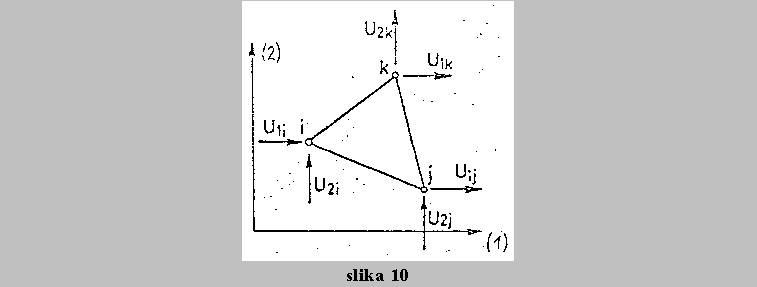
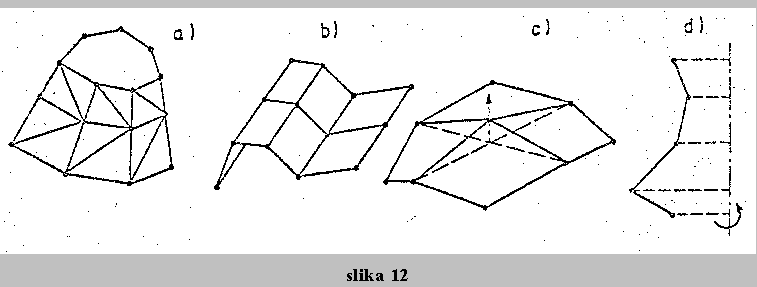
Ploskovne konstrukcije modeliramo z elementi, ki imajo dve dimenziji. Najbolj se uporabljajo trikotni in stirikotni elementi. Najbolj preprosti elementi, npr. trikotni stenski elementi imajo le 6 prostostnih stopenj, in sicer po dva pomika v vsakem vozliscu (slika 10).

Tak element uporablja poljsko matriko [a] s polinomom 1. reda. Mozno je tudi upostevati anizotropijo v materialu, ki je zajeta v matriki elasticnih konstant [E]:

sigma = E epsilon - E alpha T/(1-ni){1,1,0}^T

Tak element da konstantne specificne deformacije in napetosti po polju elementa, kar pa v primerih iz prakse pogosto ne ustreza realnemu stanju. Resitev je v zgostitvi mreze elementov, kjer se pricakujejo vecji gradienti napetosti.

Pri resevanju plosc uporabljamo elemente z vec in drugacnimi prostostnimi stopnjami. V takih primerih nas zanima pomik w v precni smeri (slika 10).

1

Najenostavnejsi trikotni ploscni element uporabi pri formiranju poljske matrike [a] polinom 3. reda, vozliscni parametri pa so w, partial w/partial x,partial w/partial y. Pomankljivost takih preprostih elementov je v tem, da ne morejo zajeti vseh robnih pogojev. Tako ni mogoce direktno zajeti robnega momenta oziroma sile na robu, ker te kolicine vsebujejo se druge in tretje odvode. Zato so se razvili elementi z vec prostostnimi stopnjami, npr. P18 in P21. Naj omenimo, da vec prostostnih stopenj pomeni tudi bistveno vecje togostne matrike in zato daljsi cas racunanja.

Pri obravnavi lupin si pomagamo z elementi, ki jih sestavimo s suponiranjem lastnosti sten in plosc. Tako nastane element L18 s po 6 prostostnimi stopnjami (3 pomiki in 3 zasuki). Togostna matrika je tedaj velikosti 18 x 18.

Uporabljajo se linearni, parabolicni in kubicni trikotni in stirikotni elementi za modeliranje plosc, membran, sten in lupin.

Pri izboru elementov se jim predpise se debelina in materialne lastnosti (fizikalne konstante materiala).

2.3 Elementi za modeliranje teles

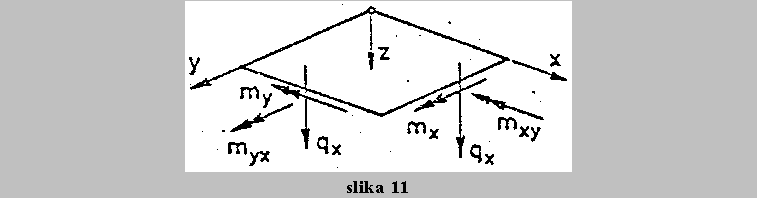
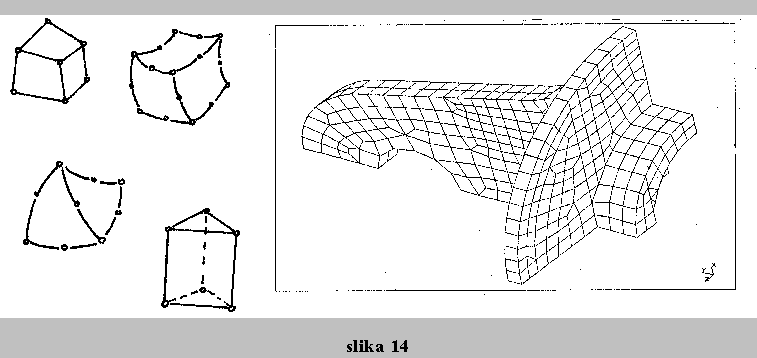
Pri resevanju kompleksnih strojnih elementov, pri tehnoloskem preoblikovanju, prevajanju toplote po telesih in drugih problemih uporabljamo tridimenzionalne elemente (slika 11).

Najenostavnejsi je stirivozliscni tetraeder, kjer ima vsako vozlisce 3 prostostne stopnje, dalje poznamo tetraedre z 10 vozlisci, kjer imamo poleg vogalnih se 6 vozlisc na sredini vsake stranice. Lahko pa bi uporabili element, ki ima v vsakem vozliscu 12 prostostnih stopenj (3 pomike in 9 zasukov. Podobne vrste elementov dobimo, ko uporabimo koncne elemente v obliki kvadrov. V praksi se uporabljajo elementi, ki so bolj ali manj deformirani, t.j. njihova oblika odstopa od idealne, se pa dobro prilegajo konturam modela konstrukcije.

Prostostne stopnje v vozliscih so le translacije v vseh smereh.

Pri opisovanju volumna je potrebno paziti, da elementi ne odstopajo prevec od svoje idealne oblike, sicer pride do tezav pri resevanju.

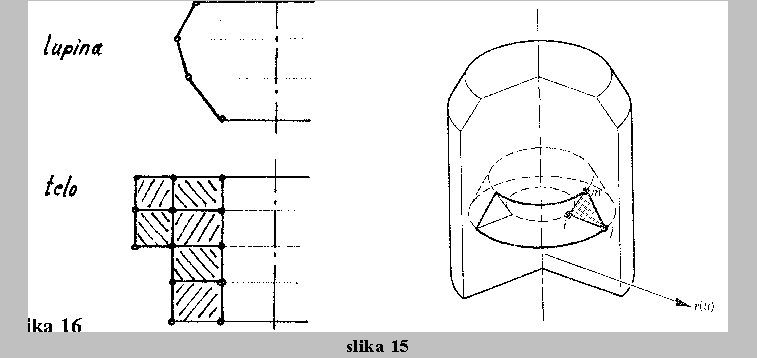
2.4 Osnosimetricne konstrukcije

V takih primerih nastopijo pri formulaciji problema z MKE dolocene poenostavitve, ki jih s pridom izkoristimo, ce uporabimo osnosimetricne elemente. Tako poznamo elemente za modeliranje rotacijskih lupin in teles.

Uporaba takih elementov obicajno predpostavlja, da so tudi robni pogoji in obremenitve osnosimetricni, nekateri proizvajalci programske opreme pa omogocajo definiranje nesimetricnih obremenitev in robnih pogojev (npr. ANSYS).

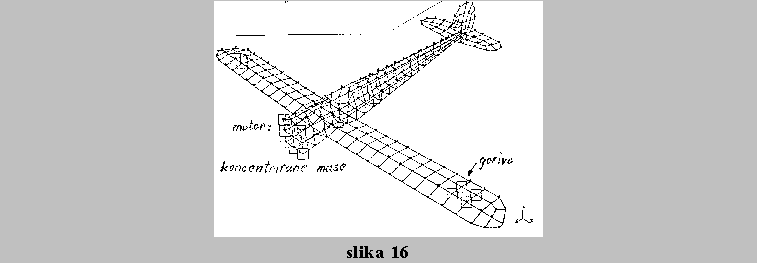
2.5 Elementi za posebne namene

Sem uvrstimo tockovne (skoncentrirane) mase (lumped mass), elemente za simulacijo trenja (gap), toge (rigid) povezovalne elemente, vzmeti (spring) in vrvi (rod), s pomocjo katerih lahko simuliramo stevilna stanja mehanike konstrukcij.

3 Posplositev metode koncnih elementov

Omenili smo, da se da z uporabo MKE resiti razlicne probleme elastostatike. Izkaze pa se, da se da metodo bistveno razsiriti. S pomocjo variacijskih metod, s katerimi po principu ekstrema minimaliziramo neko funkcijo PI (funkcional) (v primeru elastostatike imamo npr. opraviti z minimiranjem potencialne energije). Naj bo funkcija HI (potencialna energija) definirana kot integral na podrocju V (konstrukcija) in na delu robov S, ki je odvisna od funkcije {u} (pomiki) in njenih odvodov (zasuki):

ce podrocje razdelimo na manjse dele (elemente), lahko definiramo funkcijo {u} kot

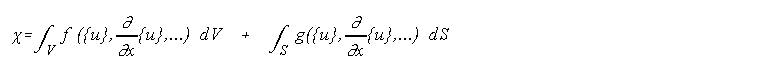{u}=[b] {U}^e .

Minimiziranje funkcionala HI glede na parametre {U} (pomike posameznih vozlisc) zahteva sistem enacb

ce lahko funkcional HI smatramo kot vsoto prispevkov posameznih delov

HI = suma HI ^e ,

potem se enacbe glasijo

V posebnem primeru, ko je HI kvadratni funkcional od {u} in odvodov, lahko vedno pisemo

kjer so [k]^e in {F}^e matrike konstant. Minimizacija sistema enacb pa postane

Vcasih se pojavi potreba po dodatnih pogojih za funkcijo {u} (robni pogoji):

G({u}) = 0

Resevanje problema sedaj zahteva minimizacijo funkcije

HI ^* = HI + lambda G

Ce so pogoji G linearni z ozirom na {u}, lahko funkcijo izrazimo kot

HI = ½{U}^T[K]{U}+{F}^T{U}+([G]{U})^T{lambda} .

Minimizacija zahteva izpolnitev naslednjih enacb

ki se resujejo z eno izmed metod za resevanje sistema (npr. LU dekompozicija).

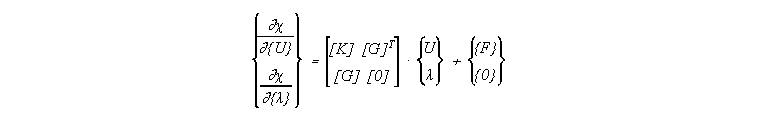3.1 Prenos toplote in termoelasticnost

Kadar zasledujemo na kontinuumu napetosti in deformacije, ki nastanejo zaradi temperaturnih obremenitev, moramo poznati porazdelitev temperature po kontinuumu. Poleg ze omenjenih enacb elastostatike moramo tedaj upostevati se enacbo prenosa toplote

k T,_ii = rho C_E T + (3 lambda + 2 µ) alpha T_o mdelta _ij (d epsilon _ij/dt).

Bistvena poenostavitev termoelasticne teorije nastopi, ce zanemarimo clen, ki vsebuje spremembo deformacij, torej epsilon=0. Taksna poenostavitev je dopustna za probleme, ki se odvijajo pocasi. Z opustitvijo dinamicnih clenov v ravnoteznih enacbah dobimo stanje, ki ga opisujemo s kvazistaticno termoelasticno teorijo, ki je neodvisna od deformacijskega stanja. Problem pa razpade na dva dela: na prenosni problem (porazdelitev temp. po kontinuumu in iskanje napetosti in deformacij pri poznani porazdelitvi temperature. Temperatura v tem primeru predstavlja zunanjo obremenitev.

3.2 Dinamika konstrukcij

Ce dodamo povrsinskim in volumskim silam telesa se vztrajnostne sile in sile, ki povzrocijo notranji upor materiala (sile dusenja) v skladu z D'Alambertovim principom dinamike, dobimo osnovno enacbo dinamike konstrukcij. Za diskretizirani kontinuum ob upostevanju vztrajnostnih in dusilnih sil dobimo osnovno enacbo koncnega elementa

{F} = [K] {U} + [C] {dU/dt} + [M] {Ü} ,

kjer je [M] masna matrika koncnega elementa, [C] pa matrika notranjega trenja (dusenja).

Masna matrika je

[M] = integral [b]^T rho [b] .

Za posamezne tipe koncnih elementov je mogoce vnaprej dolociti obrazce za sestavo masnih matrik, podobno kot to velja za togostno matriko. Cesto nas pri nihanju sistemov zanimajo samo nihanja v doloceni smeri, pa se v teh primerih masne matrike ustrezno poenostavijo.

Pri preucevanju dinamicnih problemov na konstrukcijah so med najpomembnejsimi problemi nihanja sistemov. Nihanja so lahko lastna, vsiljena, lahko so dusena ali nedusena.

3.2.1 Lastna nihanja

Za lastna nedusena nihanja je znacilna naslednja enacba

[M] {Ü} + [K] {U} = 0 .

Ker so taka nihanja harmonicna, lahko predpostavimo vozliscni vektor {U} v obliki

{U} = {q} e^{i omega t}

Ce nastavek uvrstimo, dobimo karakteristicno enacbo lastnega nihanja

(-omega² [M] + [K] ) {q} = {0}

Ta homogeni sistem enacb je resljiv za {q} le, ce velja

det | -omega² [M] + [K] | = {0}

Iz tega pogoja je mogoce dolociti frekvence omega lastnih nihanj. Nadalje je ob poznavanju omega mozno dolociti amplitudne vektorje {q} (lastne vektorje), ki predstavljajo relativne pomike konstrukcije.

Stevilo lastnih frekvenc omega sledi iz stevila prostostnih stopenj masne oziroma togostne matrike. V praksi nastopajo matrike relativno velikih rangov in je potrebno stevilo prostostnih stopenj omejiti. To v praksi izvedemo tako, da na konstrukciji dolocimo primerno stevilo tock, ki so sposobne nihanj v dolocenih smereh. Stevilo prostostnih stopenj je tako neprimerno manjse in iskanje lastnih frekvenc hitro konvergira.

3.2.2 Vsiljena nihanja

Kadar na sistem, ki je sposoben nihanja, deluje neka sila, ki je v splosnem odvisna od casa, govorimo o vsiljenem nihanju. Ce zanemarimo dusenje, je

[M] {Ü} + [K] {U} = { F(t) }

Vsiljena sila {F(t)} je lahko periodicna, casovno spremenljiva funkcija, lahko pa je tudi povsem poljubna obremenitev sistema. Sistem sledi tej obremenitvi in opravlja pri tem t.i. odzivna nihanja. Resevanje po direktni poti je neugodno, saj imata matriki [M] in [K] izvendiagonalne clene. Postopek se obcutno poenostavi, ce uporabimo modalno analizo, ki prevede omenjene enacbe v take, ki so med seboj neodvisne.

Podrobnejsa analiza pokaze, da se da odziv sistema popisati s pomocjo Duhamelovega integrala:

kjer je P(tau) vzbujevalna sila. Za nekatere funkcije P(tau) je integral resljiv v zakljuceni obliki, sicer pa uporabimo numericne metode.

3.3 Stabilnostni problemi

Stabilnost konstrukcij obravnava nelinearne probleme mehanike, ki izhajajo iz geometrijske nelinearnosti. Take nelinearnosti proucujemo s teorijo velikih deformacij. Za specificne deformacije upostevamo nelinearni clen:

epsilon _ij = ½(u_i,j + u_j,i + u_i,ju_j,i )

V matricni obliki je tedaj

{epsilon} = [d]{u} = [d][b]{U} = [B]{U} ,

kjer vsebuje [B] nelinearne clene. Enacbo koncnega elementa zapisemo takole:

integral [B]^T {sigma} dV - {F} = 0

oziroma simbolicno

{KSI({U})} = 0 .

Zvezo med funkcijo KSI in vektorjem {U} dobimo, ce enacbo variramo. Rezultat simbolicno zapisemo kot splosno stabilnostno enacbo:

d{KSI} = ( [K] + [K^G] + [K^L] ) d{U} ,

kjer je [K] poznana togostna matrika, [K^G] geometrijska matrika in [K^L] matrika velikih deformacij. Vsota matrik tvori tangentno matriko. Ker enacba vsebuje nelinearne clene, jo resujemo z iteracijskimi metodami, pogosta je Newtonova iteracijska metoda.

Pri uklonu palic, nosilcev, plosc in lupin nastopajo pri idealni geometriji stabilnostni problemi, ki jih imenujemo zacetna stabilnost. V takih primerih je geometrijska matrika proporcionalna obremenitvi, ce pa se zanemarimo vpliv matrike [K^L] lahko stabilnostno enacbo zapisemo v obliki

d{KSI} = ([K] + [K^G]) d{U} = 0

Ce narasca obremenitev tako, da je proporcionalna faktorju , dobimo nevtralno stabilnost, ce pisemo

([K] + lambda [K^G]) d{U} = {0}

Netrivialna resitev obstaja v primeru

det | [K] + lambda [K^G] | = {0} .

Faktor lambda imenujemo tudi kriticna uklonska sila. Le-to dolocimo po postopku, ki je analogen iskanju lastnih frekvenc sistema.

3.4 Problemi plastomehanike

Teorijo majhnih deformacij uporabljamo v konstrukcijski mehaniki strojniskih in gradbenih naprav in konstrukcij, ki zaradi velikih deformacij ne bi mogle normalno obratovati. Nelinearnost teorije elasto-plasticnih deformacij pa izvira iz eksperimentalno dolocenih zvez med napetostmi in deformacijami. Taksno zvezo imenujemo fizikalna nelinearnost oziroma materialna nelinearnost.

Za formulacijo takih problemov princip virtualnih pomikov ni uporaben. Tako je zvezo med napetostmi in deformacijami potrebno odsekoma linearizirati. Enacba koncnega elementa pa bo dobila obliko

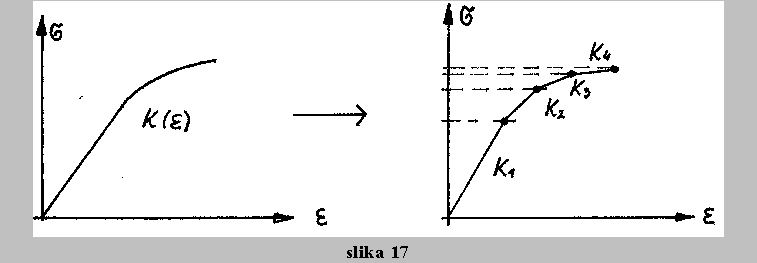[K] {dU} = {dF} ,

kjer sta {dF} in {dU} prirastka obremenitve oziroma pomikov. V plasticnem obmocju bo tudi togostna matrika dobila novo vrednost, namrec

[K_p] = integral [p]^T[E_ep][p] dV ,

kjer je [E_ep] ustrezna elasto-plasticna matrika. Sistem enacb konstrukcije je potrebno resevati v majhnih korakih:

[K]⁽ⁿ⁾ {vdelta U}⁽ⁿ⁺¹⁾ = {vdelta F}⁽ⁿ⁾

{U}⁽ⁿ⁺¹⁾ = {U}⁽ⁿ⁾ + {vdelta U}⁽ⁿ⁺¹⁾ ,

kjer je (n) dolocen korak v iteracijskem postopku. [K]⁽ⁿ⁾ dobimo iz vrednosti [E_ep] na zacetku n-tega koraka, {vdelta F}⁽ⁿ⁾ iz zacetnih podatkov in {vdelta U}⁽ⁿ⁺¹⁾ iz sistema enacb.

4 Literatura

Prelog E., Metoda koncnih elementov

Zienkiewics O. C. , The Finite Element Method in Engineering Science, 1971, McGraw-Hill

Sekulovi M., Metod Konacnih Elemenata, 1988, IRO Graevinska knjiga Beograd