Analiza vodnega toka
Trdnostna analiza
Zakljucek
Uvod
Porocilo obravnava pristop k trdnostni analizi geometrijsko kompleksne komponente, kot je gonilnik Francisove
turbine. Analizirana sta bila dva francisova gonilnika
ns =100 (HE Torro) in
ns =415 (HE Stratos). Namen raziskave
je posodobiti trdnostni preracun najbolj obremenjenih delov. Ce bi obstajal parametricni popis komponent za celotno
podrocje ns, ki ga pokriva proizvajalec turbin, bi taka dokumentacija utegnila povecati konkurencnost proizvajalca
turbin na naslednje nacine:
- - krajsi cas izdelave ponudb
- - bolj popolna dokumentacija ponudbe, realnejsa ocena stroskov
- - krajsi cas izdelave konstrukcijske dokumentacije
- - zanesljivejsa ocena aksialne sile (gred, aksialni lezaj!)
- - zmanjsanje stroskov za kontrolo (ni potrebna 100% kontrola za manj obremenjene lokacije na komponentah)
- - zanesljivejse obratovanje
- - napoved obnasanja pri prehodnih pojavih
- - prihranek materialnih in tehnoloskih stroskov z manjsimi dimenzijami turbine
Zaradi zapletenih geometrijskih oblik in raznolikosti obremenitev je bila uporabljena numericna simulacija. Za
simulacijo vodnega toka je bila uporabljena metoda koncnih volumnov, za trdnostno analizo pa metoda koncnih
elementov. Rezultat takega pristopa so izdelava ustrezne konstrukcijske dokumentacije (zahteva narocnika projekta)
in predlagane modifikacije ze v fazi konstrukcije.
ANALIZA VODNEGA TOKA
Analiza napetostno-deformacijskega stanja konstrukcij zahteva poleg poznavanja geometrije konstrukcije se
poznavanje obremenitvenih stanj. Za vodne stroje je znacilno, da poleg obicajnih sil (lastna teza, centrifugalna sila)
nastopajo obremenitve vsled toka vode, ki tece skozi kanale komponent stroja. V gonilnikih Francisovih turbin se
tako srecujemo z obremenitvami lopat, pri cemer je odlocilna porazdelitev in velikost tlaka po lopati. To tlacno polje
pa je odvisno od rezima obratovanja turbine (pretoka, odprtosti vodilnika, vrtincev za rotorjem itd.). Znacilno je, da
so podatki o porazdelitvah redki v literaturi in niso sistematicno obdelani za npr. razlicne specificne vrtilne hitrosti.
se bolj redko pa naletimo na podatke o opravljenih meritvah, ki bi predvidevanja potrdila. Ker so poleg centrifugalne
sile porazdelitve tlakov kljucnega pomena (se posebno pri velikih in vitkih gonilnikih), je nujna dolocitev take
porazdelitve za vsak gonilnik posebej.
Do porazdelitve tlakov je mozno priti preko porazdelitve hitrosti. Obstajajo analiticne metode, ki obravnavajo bolj
ali manj idealen tok fluida (brez vrtincev). V novejsem casu pa se vse vec uporabljajo numericne metode, kot so
metoda koncnih in metoda robnih elementov, metoda koncnih diferenc, metoda koncnih volumnov, metoda diskretnih
vrtincev (za dvodimenzionalne probleme) in metoda ukrivljenih tokovnic. Za popis toka v kanalu rotorja se izkazejo
primerne le metode, ki obravnavajo problem tridimenzionalno.
Opis metode resevanja
Zaradi zapletenih prostorskih in hidrodinamicnih razmer je pri dolocitvi porazdelitve tlakov smiselno uporabljati
numericno simulacijo vodnega toka. V praksi se za tovrstne analize najvec uporabljata metoda koncnih elementov
in metoda koncnih volumnov zaradi relativno enostavne diskretizacije racunskega obmocja in splosnega 3D pristopa.
Izkaze se, da je MKV bolj primerna za take analize. Na trziscu obstaja vec proizvajalcev programske opreme, ki so
specializirane za hidravlicne preracune - racunsko dinamiko fluidov
(Computational Fluid Dynamics - CFD). V tej raziskavi je bilo uporabljeno
programsko orodje TASCflow programske hise Advanced Scientific Computing Ltd-ASC (Waterloo, Ontario,
Canada), ki tece na racunalniku CONVEX 3860 (Institut Jozef Stefan).
Temeljne enacbe, ki jih resujejo CFD programi, so casovno povprecene Navier-Stokesove enacbe, ki izhajajo iz
zakonov o ohranitvi mase, gibalne kolicine in energije
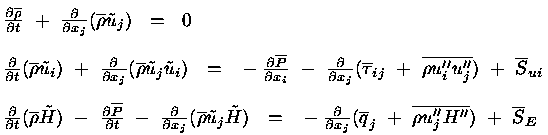
Prva enacba je kontinuitetna, druga je vektorska za ohranitev gibalne kolicine, tretja pa je
energijska enacba, kjer pomenijo
- ui hitrosti v x1-x2-x3 kartezicnem koordinatnem sistemu
- P je staticni tlak
- E celotna energija in H entalpija
- ro je gostota
- Tauij je viskozni napetostni tenzor
- qi oznacuje energijo prevoda toplote
- S so dodatni izvori energije
Reynoldsove napetosti ui''uj'' in tok turbulentne energije ui''H'' pa se ne dasta izraziti s srednjimi vrednostmi
spremenljivk. Zato je potrebno uporabiti dodatne enacbe, ki jih opisuje npr. K-eps model.
Priprava podatkov
Analiza vodnega toka v kanalih francisove turbine zahteva poleg poznavanja geometrije kanalov se poznavanje
tokovnih razmer tudi v delu pred lopato in za lopato. Zato je potrebno modelirati del vodnega toka nekaj pred
gonilnikom, v kanalu gonilnika in del toka v sealni cevi. Analiziran je bil gonilnik
ns=100, kjer je medprostor med
vodilnimi in gonilnimi lopaticami majhen. To dejstvo poenostavi vstopne robne pogoje, saj smemo
predpostaviti na vstopu v gonilnik kar smer in velikost toka na izstopu iz vodilnika.
Problem nadalje poenostavimo, ce predpostavimo periodicnost toka (zaradi periodicne geometrije vodilnika in
gonilnika. Slika prikazuje gonilnik in racunsko obmocje, ki nas zanima.

V podrocje razporedimo vozlisca koncnih volumnov.Na tako pripravljeni strukturirani mrezi
definiramo robne pogoje oziroma povemo, kaksno je stanje na mejah
racunskega podrocja. Stanje na vstopu v gonilnik je mozno predpostaviti, ce poznamo geometrijo
vodilnika in tokovne razmere v njem. Iz ustreznih risb vodilnika in podatkov o polozaju lopatic za dolocen rezim
obratovanja ocenimo velikost in smer hitrosti na vstopu v racunsko obmocje.
Na ustreznih parih povrsin predpisemo periodicne robne pogoje (identicna porazdelitev tlakov, turbulentnih
velicin, periodicna porazdelitev hitrosti, ...).
Ravno slednja prepostavka slabo drzi v realnih strojih, saj je pri francisovih gonilnikih znacilen pojav vrtinca za
gonilnikom. Pojav je izrazito nestacionaren (casovno odvisen) in ga ni mogoce opisati z enostavnimi modeli, kot je
nas.
Parametri resevanja
Ce pri resevanju upostevamo dolocene poenostavitve, se lahko obseg racunanja znatno zmanjsa. Za nas primer
predpostavimo:
turbulentnost toka
nestisljivost
izotermicnost
stene (meje podrocja) rotirajo
Resevanje poteka z iteracijami. Pri resevanju enacb se pojavljajo ostanki, ki predstavljajo neko napako. Natancnost
resevanja lahko predpisemo z npr. maksimalnimi ostanki pri iteracijah R oziroma RMS R na npr.
10-3, hkrati pa
obicajno omejimo tudi absolutno stevilo iteracij (ce npr. resevanje pocasi oziroma ne konvergira).
Kadar iscemo resitve stacionarnega problema, predpisemo casovni korak, ki zagotovi ucinkovit relaksacijski
postopek. Relaksacija je potrebna, ker gre za resevanje nelinearnega problema kot zaporedja linearnih problemov.
Vloga casovnega koraka postane bolj pomembna pri mocno nelinearnih in casovno odvisnih problemih.
Pred resevanjem poskrbimo se za izhodiscno stanje za iteracije - predpisemo npr. porazdelitev hitrostnega polja.
Rezultati
Priprava podatkov za resevanje (modeliranje racunskega obmocja, diskretizacija, prenos podatkov na drug
racunalnik, definiranje robnih pogojev in drugih parametrov) je trajala ~50 ur.
Na racunalniku CONVEX 3860, verzija programa TASCflow 2.3 - neparalelna, stevilo iteracij 20, dosezena natancnost Rmax je reda
velikosti 10-3, RMS-R reda velikosti 10-4, je trajalo resevanje opisanega modela 20 minut (CPU).
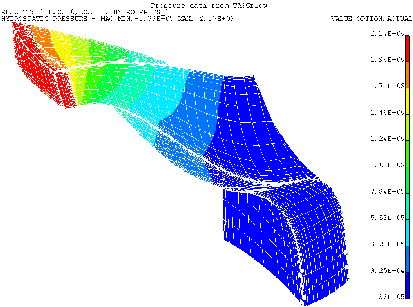
Rezultat nase analize vodnega toka so porazdelitve hitrosti in tlakov v racunskem podrocju. Porazdelitev hitrosti za
nas primer kaze slika. Se posebej nas zanimajo porazdelitve tlaka na stenah lopat.
Potek tlakov vzdolz kanala prikazemo v obliki kontur na povrsini lopate.
TRDNOSTNA ANALIZA
Teorija mehanike opisuje obnasanje konstrukcij z diferencialnimi enacbami. Vendar pa postane za zahtevano
natancnost izracunov teorija neuporabna, saj privede upostevanje in definiranje ukrivljenosti ter nestandardnih robnih
pogojev do velikih komplikacij. Zato se v praksi uporabljajo izkljucno numericne metode, najvec metoda koncnih
elementov. Na trziscu obstaja cela vrsta programskih paketov, s pomocjo katerih je bolj ali manj enostavno mogoce
problem definirati in priti do uporabnih rezultatov. Med najbolj znanimi in splosnimi so npr. MSC-NASTRAN,
ANSYS, ABAQUS, IDEAS, MARC, COSMOS, ... V pricujoci nalogi je bil uporabljen programski paket I-DEAS
(Structural Dynamics Research Corporation - SDRC, Cincinatti, Ohio), ki je instaliran na racunalnikih HP 735
in INDIGO 2 v laboratoriju LECAD, Fakulteta za strojnistvo.
Metoda kocnih elementov je med inzenirji dobro znana in uveljavljena in se da aplicirati na sirsa podrocja mehanike
in fizike, kot so elasto- in plastomehanika, prenos toplote, dinamika konstrukcij, stabilnost, hidromehanika, podrocja
geomehanike itd. Temelji na diskretizaciji poljubne konstrukcije oziroma obmocja na koncne elemente ustreznega
tipa in uporabi matricne algebre. Elementi so med seboj povezani preko vozlisc z ustreznim stevilom prostostnih
stopenj. Diferencialne enacbe, ki popisujejo obnasanje konstrukcije (najbolj splosne so energijske enacbe),
diskretiziramo po vozliscih, upostevamo fizikalne in materialne lastnosti elementov ter jih zapisemo v matricni obliki.
Na enak nacin izrazimo se robne pogoje (vpetja konstrukcije, simetrije in druge matematice pogoje) ter obremenitve
(zunanje sile, tlake na ploskvah, masne sile). Z uporabo matricne algebre je nato mogoce izracunati vse neznane
velicine (napetosti, deformacije, lastne frekvence). Matricne operacije so pri velikem stevilu elementov (vozlisc)
izredno obsezne, zato so dobrodosli cim hitrejsi racunalniki z velikimi spominskimi kapacitetami. Med inzenirji so
se uveljavili kriteriji, s katerimi popisujemo velikost racunskega problema. Eden izmed kriterijev oziroma ocena v
elastomehaniki je velikost togostne matrike, oziroma najvecje stevilo potencialno nenicnih elementov merjeno od
diagonale do prve nicle - sirina pasu togostne matrike (wavefront, Maximal Matrix Nodal Half Bandwidth
MMNHB). Po drugi strani pa se od racunalnikov pricakuje velika graficna moc, saj vecino casa (90-95% pri danasnji
opremi) uporabnik nameni pripravi modela (definiranje 3D geometrije in diskretizacija v mrezo koncnih elementov -
mrezenje) in predstavitvi rezultatov (predelava numericnih rezultatov v graficno - barvno obliko).
Cilji trdnostne analize
Pri trdnostnih analizah komponent vodnih turbin gre predvsem za dolocitev napetosti in deformacij, ki nastanejo kot
posledica obremenitev z vodnim tlakom in centrifugalno silo. Vcasih narocnik zahteva se upostevanje lastne teze in
potresnih sil. Centrifugalna sila ima se posebno velik vpliv pri pobegu turbine, ko se obrati gonilnika mocno zvisajo.
Pri velikih gonilnikih utegnejo nastati tudi bocne obremenitve vsled lezajnega efekta zaradi ekscentricnosti gonilnika
in labirintnih tesnil na statorju. V gradnji turbin so se uveljavili kriteriji o dopustnih napetostih.
Pri normalnih obratovalnih pogojih je dopustna napetost za gonilnik,
spiralno ohisje in predvodilne lopate

Za izredne pogoje pa
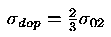
Konstrukcija mora biti zasnovana tako, da pri predpostavljenih obremenitvah dopustne napetosti niso presezene.
Analiza pokaze kriticna mesta, naloga konstrukterja pa je, da konstrukcijo preoblikuje tako, da bo kriterijem
zadosceno. Vcasih pa to ni mozno, npr. zaradi poslabsanja hidravlicnih karakteristik komponent, ki so v stiku z vodo.
Tedaj je poleg variranja tehnologije mozno uporabiti boljse materiale.
Vcasih je trdnostni kriterij lahko tudi deformacija, ki je se dopustna, da se komponenti ne zmanjsa funkcionalnost.
Izkaze se, da pride npr. pri Kaplanovih turbinah do znatne deformacije lopate v aksialni in posledicno v radialni smeri
na zunanjem robu (konzolno vpetje lopate). Zaradi majhnih toleranc je dolocitev take deformacije lahko izrednega
pomena.
Poleg trdnostne analize se pogosto zahtevajo tudi dinamicne karakteristike, izmed katerih je (praviloma z uporabo
numericnih metod) najenostavnejse dolociti lastne frekvence in oblike strukture. Cilj je izognitev frekvencam
vzbujanja. Inzenirji se posluzujejo kriterija, ki popisujejo mozne frekvence vzbujanja
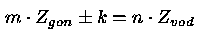
kjer je
Zgon stevilo lopat gonilnika,
Zvod stevilo lopat vodilnika,
m in n sta poljubni naravni stevili,
k je stevilo diametralnih vozlov (stevilo valov po obsegu - lastna oblika nihanja).
Ta vzbujanja nastajajo kot posledica prehoda
lopate gonilnika mimo lopate vodilnika. V splosnem zahtevajo lastne oblike z k >> 1 veliko energije oziroma
nastopijo pri visokih frekvencah. Raziskovalci porocajo o zaznavanju lastnih oblik oziroma frekvenc, ki ustrezajo
vrednostim k = 1..4.
Po zbrani literaturi zaenkrat ne obstajajo metode za teoreticno dolocevanje amplitude napetosti. Je pa mozno izogniti
se potencialnemu vzbujanju s prilagoditvijo stevila lopat vodilnika oziroma gonilnika ter s spremembo togosti
oziroma mase sodelujocih komponent.
Geometrija in diskretizacija
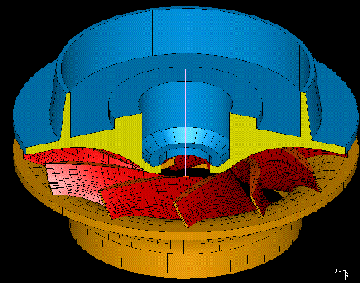 Geometrija venca in pesta (rotacijski telesi) se prepiseta iz ustrezne konstrukcijske dokumentacije (praviloma 2D
risbe). Za popis lopate pa se je uveljavil nacin, pri katerem posredujemo mnozico tock, popisanih z x-y-z oziroma
r-fi-z koordinatami. Ti podatki so namrec na voljo ze pri izdelavi NC programov, s takim nacinom popisovanja pa
se tudi izognemo tezavam kompatibilnosti 3D modelirnikov.
Geometrija venca in pesta (rotacijski telesi) se prepiseta iz ustrezne konstrukcijske dokumentacije (praviloma 2D
risbe). Za popis lopate pa se je uveljavil nacin, pri katerem posredujemo mnozico tock, popisanih z x-y-z oziroma
r-fi-z koordinatami. Ti podatki so namrec na voljo ze pri izdelavi NC programov, s takim nacinom popisovanja pa
se tudi izognemo tezavam kompatibilnosti 3D modelirnikov.
Pri mrezenju upostevamo dejstvo, da je geometrija gonilnika periodicna (ciklicno simetricna), v smislu, da se dolocen
del gonilnika (ena lopata in pripadajoci del pesta ter venca) ponavlja okoli osi rotacije. Ker predpostavljamo, da je
tudi obremenitev periodicna, smemo pri uporabi posebnih, ciklicnih robnih pogojev obravnavati le en segment
geometrije.

Tip elementa izberemo glede na dimenzije posameznih sestavnih delov rotorja ter glede na zahtevano natancnost
izracuna. Za masivni rotor ns =100 izberemo volumske kvadraste linearne (8 vozliscne) elemente, medtem ko za
ns =415 izdelamo analize z razlicnimi tipi - npr. samo volumskimi in kombinacijo volumskih in lupinskih.
Robni pogoji in obremenitve
V primeru staticnih obremenitev, ki se ponavljajo enako kot geometrija, mora deformacija odrazati to periodicnost
in mora biti enaka v vseh segmentih. Zato mora biti posplosena deformacija na desnem simetrijskem robu enaka
deformaciji na levem:
{u} desni =
{u} levi
To pomeni, da morajo biti posamezne komponente deformacij paroma (na levi in desni) enake v cilindricnem
koordinatnem sistemu, ki definira simetrijo (kar os rotacije).
Nadalje je gonilnik pritrjen na turbinsko gred, ki prevzame vrtilni moment in aksialno silo. Zaradi periodicne
obremenitve v modelu se radialne sile med seboj kompenzirajo, tako da je potrebno podprtje modela na mestih
pritrditve na gred le v tangentni in aksialni smeri. Zaradi velike togosti mesta pritrditve je opisani nacin
upravicen za staticno analizo in opazovanje stanja dalec od pritrditve. Vendar utegne biti vprasljiv pri npr. dinamicni
analizi pri dolocitvi prve lastne oblike, torej najnizje lastne frekvence.
Pri normalnih pogojih obratovanja je gonilnik podvrzen dvema tipoma obremenitev, namrec staticnemu pritisku vode
na lopate in centrifugalni sili kot posledici vrtenja. Porazdelitev tlaka vode je dolocena z analizo toka.
Porazdelitev tlaka lahko shematicno prikazemo v treh dimenzijah, pri cemer predstavlja oddaljenost povrsine P1 od
povrsine lopate vrednost tlaka (podajanje z interpolacijskim skalarnim poljem).
Centrifugalno silo opredeljuje hitrost vrtenja, oddaljenost diskretiziranih mas od sredisca vrtenja in velikost
(porazdelitev) mas. Izracun posameznih prispevkov (za vsak element-vozlisce posebej) je avtomatiziran in ga
prepustimo programskemu orodju in integriranemu izracunavalniku.
V primeru pobega turbine postane obremenitev s tlakom vode zanemarljiva v primerjavi s centrifugalno silo, tako
da se za take primere obicajno uposteva le slednja obremenitev.
Rezultati staticnih obremenitvenih primerov
Tako pripravljeni modeli se posredujejo izracunavalniku, to je delu programskega orodja, ki podatke pretvori v matricno
obliko, aplicira zakone mehanike in izracuna zahtevane velicine. V nasem primeru je bil uporabljen linearni staticni
solver, rezultati pa so izracunani v obliki napetosti, deformacij in reakcij.
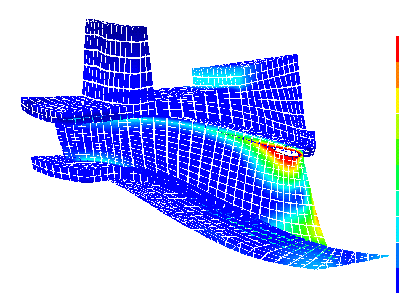
Priprava modela TORRO (modeliranje geometrije, diskretizacija, definiranje robnih pogojev in drugih parametrov)
je trajala ~70 ur. Resevanje staticnih obremenitvenih primerov na opremi HP 735 pa ~3 ure.
Za Francisove gonilnike je v splosnem znacilno, da se pesto in venec malo deformirata v primerjavi z lopato.
Prevladujoca je torzijska deformacija gonilnika, katere posledica so znacilna obmocja koncentracij napetosti na lopati
v blizini izstopnega roba na spoju s pestom ter povecane napetosti na prvi tretjini lopate v blizini spoja s pestom
. Za hitrovrtece gonilnike utegne biti prispevek napetosti zaradi centrifugalne sile vecji od
prispevka vsled vodnega tlaka.
Predlagane spremembe konstrukcije
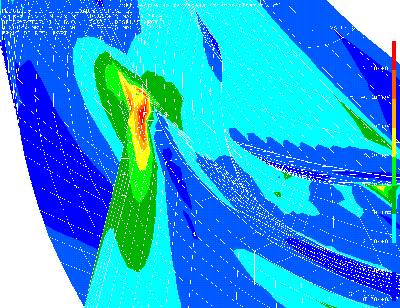 Pokanje lopat na gonilnikih STRATOS v blizini spoja lopate s pestom na izstopnem robu med dejanskim
obratovanjem turbine kaze na znatne napetosti na tem mestu. V pomanjkanju meritev pa je dejansko velikost
napetosti tezko dolociti iz naslednjih razlogov:
neznane porazdelitve tlakov v razmerah, ki niso optimalne
neznane amplitude nihanja gonilnika in posledicne neznane dinamicne obremenitve
neznane zaostale napetosti kot posledica tehnologije izdelave
drugi vplivi (nestacionaren in neperiodicen tok vode za gonilnikom, vprasljiva velikost lezajnega efekta)
Pokanje lopat na gonilnikih STRATOS v blizini spoja lopate s pestom na izstopnem robu med dejanskim
obratovanjem turbine kaze na znatne napetosti na tem mestu. V pomanjkanju meritev pa je dejansko velikost
napetosti tezko dolociti iz naslednjih razlogov:
neznane porazdelitve tlakov v razmerah, ki niso optimalne
neznane amplitude nihanja gonilnika in posledicne neznane dinamicne obremenitve
neznane zaostale napetosti kot posledica tehnologije izdelave
drugi vplivi (nestacionaren in neperiodicen tok vode za gonilnikom, vprasljiva velikost lezajnega efekta)
Vendar pa je mogoce s pomocjo opisane trdnostne analize sklepati na potrebne modifikacije in nato primerjati
napetosti na originalu in modificirani konstrukciji. Zaradi pomembnosti rezultatov je bil zato zgrajen bolj popoln
model gonilnika s 7056 elementi in 9468 vozlisci, kjer so bili upostevani konstrukcijski detajli (npr. radiji zaokrozitve
spoja lopate in pesta). Glede na izkazano deformacijo gonilnika smemo sklepati na potrebne spremembe, ki bi
utegnile znizati nivo napetosti v kriticnih mestih. Predlagana sprememba je odebelitev lopate na sirsem podrocju
koncentracij.
 Taka sprememba omili konico napetosti za ~18%. Zaradi
neposredne blizine pesta, vpihavanja zraka v tok vode pod rotorjem in dejstva, da se vecina energije vode pretvori
v mehansko na zunanjem delu lopate, smemo sklepati, da omenjena modifikacija ne vpliva na hidravlicne
karakteristike stroja.
Taka sprememba omili konico napetosti za ~18%. Zaradi
neposredne blizine pesta, vpihavanja zraka v tok vode pod rotorjem in dejstva, da se vecina energije vode pretvori
v mehansko na zunanjem delu lopate, smemo sklepati, da omenjena modifikacija ne vpliva na hidravlicne
karakteristike stroja.
Dolocitev napetosti pri delovanju bocne sile na gonilnik
Iz prakse je znano, da zaradi ovalnosti gonilnikov in labirintnih obrocev ter zaradi zamika simetrijskih osi nastopajo
bocne sile na gonilnik vsled lezajnega efekta in asimetricnega aksialnega toka vode skozi labirinte. Te sile so pri HE STRATOS reda E+3 N, pri HE TORRO pa E+4 N.
Vendar utegnejo biti sile vsled aksialnega toka vode skozi spodnje labirinte mnogo vecje. Velikost teh sil lahko pri
dani geometriji in padcu tlaka na gonilniku ocenimo z izrazom

kjer je R radij obroca, c_1 je zracnost na zgornjem labirintu, c_2 je zracnost na spodnjem labirintu,
e je vsota sirine tol. polja za gonilnik, delta p pa je padec tlaka. Za HE STRATOS je pri e = 2 mm sila reda E+4 N. Da bi ugotovili, kaksne posledice ima to na napetostni sliki,
zgradimo model celotnega gonilnika. Ker gre za oceno, se zadovoljimo z lupinskimi elementi. Srednje ploskve pomrezimo s 3660 lupinskimi linearnimi stirikotnimi elementi, ki jih povezuje 3760 vozlisc,
velikost racunskega modela pa je MMNHB = 724.
Izkaze se, da najvecje napetosti zopet nastopijo na spoju lopate z pestom na izstopnem robu, vendar so napetosti zelo
majhne - reda 1 N - in so zanemarljive v primerjavi z napetostmi pri delovanju vodnega tlaka na lopatah.
Dolocitev lastnih frekvenc in oblik
Za dolocevanje lastnih frekvenc in oblik diskretnih modelov obstaja vec algoritmov. Med uporabniki
MKE se najvec uporablja Guyan-ova redukcija. Gre za to, da se pri velikih modelih reducira stevilo enacb tako,
da se zmanjsa stevilo diskretnih mas. Metoda zahteva od uporabnika, da na podlagi izkusenj sam oceni stevilo in
razporeditev diskretnih mas. Splosno pravilo je, da se mase postavijo v tiste tocke, kjer se pricakujejo najvecje
amplitude nihanj.
Poleg omenjene metode obstaja se vec drugih, npr. simultana vektorska iteracija (SVI), ki
je posebno primerna za velike modele in ima dobro konvergenco predvsem za nizje lastne frekvence.

Modela, ki smo ju uporabljali za staticne obremenitvene primere, ne dasta prave slike o dinamicnem obnasanju, saj
lahko s takimi modeli popisemo le tiste lastne oblike, ki so iste na vseh segmentih, torej se periodicno ponavljajo.
Nekateri izracunavalniki omogocajo izracune lastnih oblik celotnih rotorjev, pri
cemer izhajajo iz modela le enega segmenta. Programsko orodje I-DEAS zal tega ne omogoca, zato je potrebno
zgraditi model celotnega rotorja. Ta model je bil analiziran z metodo SVI (MMNBH=2617, cas
racunanja ~ 3 ure).
Najnizja lastna frekvenca je tista, pri kateri se gonilnik ziblje kot zvon. Lastna oblika je odvisna predvsem od nacina,
kako je gonilnik vpet (kar pa ni najbolje modelirano).
Potem nastopa torzijsko gibanje gonilnika, ki ga je mogoce
prevideti z obema modeloma (tako enim segmentom kot celotnim modelom). Nato nastopa lastna oblika z dvema
valoma v obodni smeri. Zatem pride do aksialnega gibanja, kjer se rob pesta in rob venca gibljeta v isti (aksialni)
smeri.
Za bolj natancne napovedi obnasanja gonilnikov med obratovanjem bi bilo potrebno upostevati dejstvo, da je
gonilnik potopljen v vodi. Obstajajo studije, ki poskusajo dolociti maso vode, ki sodeluje pri nihanju gonilnika in
celo poskusajo upostevati hitrost fluida. Vendar so ta teoreticna razglabljanja redko podkrepljena z meritvami, ki bi
dokazovala pravilnost domnev. Nekateri raziskovalci porocajo, da se lastna frekvenca gonilnikov, ki so potopljeni
v vodi, zniza celo za ~50%.
Lopatice Francisovega gonilnika so nevrtljive. Zunaj optimalnega obmocja se tekocina ne prilega vec oblikam
lopatic, zato pride do odlepljanja, reciirkularnih obmocij, podrocij t.i. mrtve vode in vrtinca v sesalni cevi. Pri
obremenitvah, ki so manjse od optimuma, povzroci spiralno vrtincno jedro pulzacije tlaka v sesalni cevi, s tem pa
oscilacije padca, pretoka in elektricne moci ter neugodne vibracije in hrup, kar posredno znizuje delovno dobo stroja.
Na osnovi statisticnih podatkov obstaja ocena o frekvenci teh pulzacij f=fo/3.6, kjer je fo frekvenca vrtenja gonilnika.
Meritve so pokazale, da se frekvenca pulzacij giblje v mejah od 20 do 40 % vrtljajev gonilnika. Torej je za
konstrukcijo - predvsem za gonilnik - ugodno, ce to nevarno podrocje ne sovpade z nobeno lastnih frekvenc rotorja.
Zakljucek
Napetostna analiza gonilnikov vodnih turbin je mogoca le z uporabo numericnih metod. Za posamezen tip
gonilnika je potrebno izvesti dve vrsti preracuna: hidravlicni in trdnostni. Pri simulaciji vodnega toka se uporabijo
Navier-Stokesove enacbe za turbulentni tok, s pomocjo katerih dolocimo hitrostno oziroma tlacno polje v kanalu
gonilnika. Rezultate uporabimo v trdnostni analizi, kjer obicajno apliciramo linearne, staticne zakone mehanike
deformabilnih teles. Trdnostna analiza podaja napetostno in deformacijsko stanje na gonilniku, na podlagi katerih
je mogoce podati smernice za modifikacijo konstrukcije, ce ne zadostuje kriterijem.
Opisana obravnava zahteva relativno veliko casa, zato bi bilo smiselno izdelati preracune vnaprej za posamezne
tipe gonilnikov (oziroma vseh spremljajocih komponent). Obstojeci CAD modelirniki omogocajo parametrizacijo
oblik, tako da je mogoce izvesti serijo preracunov na topolosko podobnih gonilnikih z relativno malo uporabniskega
posredovanja in tako izbrati optimalne resitve (oblike in dimenzije gonilnika). Tak pristop bi proizvajalcu turbin
omogocil izgradnjo baze podatkov, na osnovi katere bi bilo mogoce v kratkem casu izdelati npr. tehnicne ponudbe,
izracunati stroske, izdelati celovito tehnicno dokumentacijo, itd.
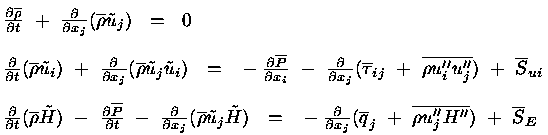
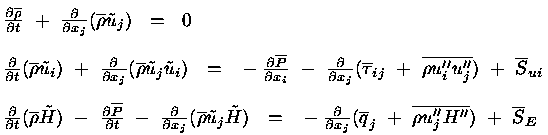



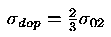
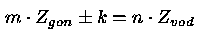
 Geometrija venca in pesta (rotacijski telesi) se prepiseta iz ustrezne konstrukcijske dokumentacije (praviloma 2D
risbe). Za popis lopate pa se je uveljavil nacin, pri katerem posredujemo mnozico tock, popisanih z x-y-z oziroma
r-fi-z koordinatami. Ti podatki so namrec na voljo ze pri izdelavi NC programov, s takim nacinom popisovanja pa
se tudi izognemo tezavam kompatibilnosti 3D modelirnikov.
Geometrija venca in pesta (rotacijski telesi) se prepiseta iz ustrezne konstrukcijske dokumentacije (praviloma 2D
risbe). Za popis lopate pa se je uveljavil nacin, pri katerem posredujemo mnozico tock, popisanih z x-y-z oziroma
r-fi-z koordinatami. Ti podatki so namrec na voljo ze pri izdelavi NC programov, s takim nacinom popisovanja pa
se tudi izognemo tezavam kompatibilnosti 3D modelirnikov.


 Pokanje lopat na gonilnikih STRATOS v blizini spoja lopate s pestom na izstopnem robu med dejanskim
obratovanjem turbine kaze na znatne napetosti na tem mestu. V pomanjkanju meritev pa je dejansko velikost
napetosti tezko dolociti iz naslednjih razlogov:
Pokanje lopat na gonilnikih STRATOS v blizini spoja lopate s pestom na izstopnem robu med dejanskim
obratovanjem turbine kaze na znatne napetosti na tem mestu. V pomanjkanju meritev pa je dejansko velikost
napetosti tezko dolociti iz naslednjih razlogov:
 Taka sprememba omili konico napetosti za ~18%. Zaradi
neposredne blizine pesta, vpihavanja zraka v tok vode pod rotorjem in dejstva, da se vecina energije vode pretvori
v mehansko na zunanjem delu lopate, smemo sklepati, da omenjena modifikacija ne vpliva na hidravlicne
karakteristike stroja.
Taka sprememba omili konico napetosti za ~18%. Zaradi
neposredne blizine pesta, vpihavanja zraka v tok vode pod rotorjem in dejstva, da se vecina energije vode pretvori
v mehansko na zunanjem delu lopate, smemo sklepati, da omenjena modifikacija ne vpliva na hidravlicne
karakteristike stroja.

