Metoda Monte Carlo

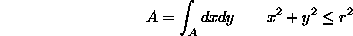
Uporaba metode Monte Carlo se omejuje na probleme, kjer imamo komplicirane robne pogoje in zahtevne funkcije, ki se ne dajo enostavno integrirati. Sama metoda je zelo enostavna vendar racunsko zelo potratna za zahtevano natancnost izracuna. Tako se za tak pristop k resevanju odlocamo le v skrajni sili, ko zelimo priblizno oceno in nimamo casa (znanje) za primernejse metode.

Oglejmo si primer resevanja povrsine kroga z radijem r = 1.

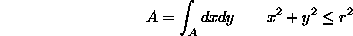
Analiticna resitev je seveda 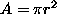. Nas krog premera d = 2 omejimo z najmanjsim pravokotnikom za katerega seveda znamo izracunati povrsimo in v katerem se stoji krog; torej 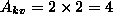. Imejmo generator nakljucnih tock, ki zagotavlja, da vsaka generirana tocka gotovo pade v pravokotnik.

Generator tako izbere recimo N tock 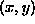. Za vsako izbrano tocko pa lahko ugotovimo ali je tocka v notranjosti kroga ali zunaj. Po razsipanju n tock smo tako ugotovili, da je sn tock padlo znotraj kroga, ostale pa so padle zunaj kroga vendar se vedno v kvadrat znanih dimenzij. Povrsino kroga laho tako brez poznavanja stevila ocenimo kot

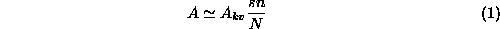
Primer: Program je posejal 100000 tock v kvadrat in ugotovil, da jih je 78589 padlo v krog. Povrsina kroga je tako

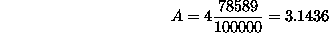
Evidentno je, da z vecanjem stevila tock dosezemo tudi dovolj natancne rezultate, vendar je za pridobitev dodatne tocne cifre potrebno vsaj deset krat vec casa. Napako metode je mozno oceniti z

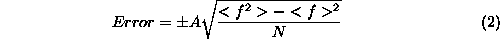
kjer puscicasti oklepaji predstavljajo aritmetico sredino preko N testnih tock.

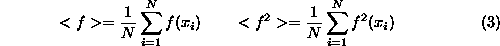
Primer programa v jeziku Fortran je sledec

        program Povrsina kroga
        n = 100000
        a = 2.0 * 2.0
        sn = 0.0
        varn = 0.0
        do 10 i = 1, n
           x = 2 * ran2(idum) - 1.0
           y = 2 * ran2(idum) - 1.0
           if ((x*x + y*y) .lt. 1.0) then
              sn = sn + 1
              varn = varn + 1
           endif
 10     continue
        print *, 'Povrsina je kroga je:', sn/n*a
        print *, 'Ocenjena napaka je:',
     *     a*sqrt((varn/n-(sn/n)**2)/n)
        end

V zanki 10 programa generirano z nakljucnim generatorjem ran2() stevila v obsegu 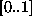in jih z mnozenjem in translacijo prestavimo v zeljeno obmocje 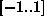. Tako generirane tocke 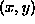testiramo na robne pogoje (kroznica) in ugotavljamo zadetek tocke v notranjst kroga. Istocasno racunamo se oceno napake za izbrano stevilo tock.

Kot generator nakljucnih stevil lahko uporabimo funkcijo random, ce je ta prikjucena v jeziku Fortran ali pa uporabimo generator ran2(), ki deluje v vsaki izvedenki jezika:

        function ran2(idum)
        parameter(m=714025, ia=1366)
        parameter(ic=150899, rm=1./m)
        dimension ir(97)
        if (idum.lt.0.or.iff.eq.0) then
           iff = 1
           idum = mod(ic - idum, m)
           do 11 j = 1, 97
              idum = mod(ia*idum + ic, m)
              ir(j) = idum
 11        continue
           idum = mod(ia*idum + ic, m)
           iy = idum
        endif
        j = 1 + (97 * iy)/m
        if (j.gt.97.or.j.lt.1) pause
        iy = ir(j)
        ran2 = iy*rm
        idum = mod(ia*idum + ic, m)
        ir(j) = idum
        return
        end

• Vztrajnostni moment kroga