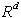 pravimo konveksen, če povezava med katerimakoli elementoma (točkama)
tega niza leži v vsej svoji dolžini v njegovi notranjosti. Najenostavnejši
niz v
pravimo konveksen, če povezava med katerimakoli elementoma (točkama)
tega niza leži v vsej svoji dolžini v njegovi notranjosti. Najenostavnejši
niz v 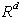 je polprostor (polravnina).
je polprostor (polravnina).Ena najbolj pogostih struktur v računski geometriji je konveksna lupina. Uporabna je kot samostojna struktura, ali pa kot pripomoček za graditev kompleksnejših struktur. V praksi se lupine uporabljajo na večih področjih. Nekatera izmed njih so: Pri določanju poti roke robota, ki je modelirana s pomočjo konveksne lupine, ko se mora ogibati ovir v prostoru delovnega giba. Pri določanju t.i. najmanjše škatle, to je najmanjša pravokotna površina oziroma prostor, kamor lahko neko konveksno lupino zapremo. Pri analizah raznih oblik, volumnov, itd.
Za prepoznavanje konveksnosti in konveksnih lupin
obstaja več različnih definicij. Nekatere izmed njih so:
1. Nizu elementov 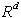 pravimo konveksen, če povezava med katerimakoli elementoma (točkama)
tega niza leži v vsej svoji dolžini v njegovi notranjosti. Najenostavnejši
niz v
pravimo konveksen, če povezava med katerimakoli elementoma (točkama)
tega niza leži v vsej svoji dolžini v njegovi notranjosti. Najenostavnejši
niz v 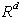 je polprostor (polravnina).
je polprostor (polravnina).
2. Konveksna lupina, sestavljena
iz niza točk S, je presek vseh polravnin, ki vsebujejo
S.
3. Konveksna lupina, sestavljena
iz niza točk S na ravnini, je najmanjši konveksni mnogokotnik,
ki obdaja niz S. V takem primeru ne obstaja noben manjši
mnogokotnik 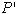 , za katerega bi veljalo
, za katerega bi veljalo 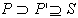 .
.
4. Konveksna lupina, sestavljena
iz niza točk S na ravnini je unija vseh trikotnikov, ki
jih določajo točke niza S.
Glavno vprašanje je, kaj se želi dobiti kot izhodni podatek. Če
se omejimo na ravnino, niz S predstavlja niz n-tih
neurejenih točk. Kot izhoden podatek je možen seznam skrajnih
točk, ali pa določena meja mnogokotnika. Skrajne točke so temena
konveksne lupine, meja pa je konveksen mnogokotnik, ki konveksno
lupino omejuje - razmejuje od okolice. Razlika je v tem, da se
s podatkom o meji dobi niz točk, ki po vrstnem redu določajo lupino,
pri seznamu skrajnih točk pa so ti podatki neurejeni.
Za določanje konveksnih lupin obstaja cela vrsta algoritmov. V
splošnem se delijo na deterministične in naključne. Tu se pokaže
prednost naključnih algoritmov, saj so v spolšnem razširljivi
na večdimenzijske prostore, medtem ko deterministični algoritmi,
ki so uporabni na ravnini, na naslednji stopnji, v prostoru odpovejo,
ali pa je njihovo izvajanje zapleteno in zelo počasno. V nadaljevanju
sta na kratko predstavljena po dva deterministična in dva naključna
algoritma.
Pri prvem determinističnem načinu je potrebno razdeliti mejo konveksne
lupine na zgornjo in spodnjo verigo (Slika 3.1).
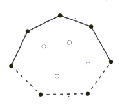
Ločnici med njima sta točki z najmanjšo in največjo vrednostjo
koordinate x. Točke iz niza N je potrebno razporediti
po naraščujoči koordinati x. Glavna ideja je, če se opazuje
samo zgornjo verigo, da se nizu 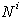 , ki vsebuje
prvih i že pregledanih točk, dodajajo naslednje, za katere
se preverja, ali ležijo na meji konveksne lupine ali v njeni notranjosti.
, ki vsebuje
prvih i že pregledanih točk, dodajajo naslednje, za katere
se preverja, ali ležijo na meji konveksne lupine ali v njeni notranjosti.
Naj bo 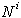 niz prvih i točk, naj bo
niz prvih i točk, naj bo
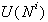 zgornja veriga, ki je že določena v okviru
zgornja veriga, ki je že določena v okviru
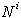 . Predpostavimo, da je del zgornje verige
. Predpostavimo, da je del zgornje verige
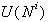 že določen. Naslednja točka, ki jo je
potrebno pregledati, je
že določen. Naslednja točka, ki jo je
potrebno pregledati, je 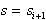 . Zadnja točka,
za katero je ugotovljeno, da je del
. Zadnja točka,
za katero je ugotovljeno, da je del 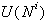 ,
naj bo r. Iz točke r se potuje po meji
,
naj bo r. Iz točke r se potuje po meji 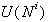 v levo in pregleduje točke na zgornji verigi. Ko se pregleda točka
q, je pregledovanje končano, saj leži naslednja točka p
pod linijo sq. Očitno je, da je v zgornjo povezavo
v levo in pregleduje točke na zgornji verigi. Ko se pregleda točka
q, je pregledovanje končano, saj leži naslednja točka p
pod linijo sq. Očitno je, da je v zgornjo povezavo 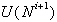 potrebno pripisati povezavo med točkama s in q ter
zbrisati vse točke iz
potrebno pripisati povezavo med točkama s in q ter
zbrisati vse točke iz 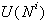 , ki so desno od
točke q (Slika 3.2). Enak postopek je potrebno ponoviti
za določanje spodnje verige.
, ki so desno od
točke q (Slika 3.2). Enak postopek je potrebno ponoviti
za določanje spodnje verige.

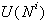 ;
(b)
;
(b) 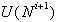 .
.
Drugi determinističen algoritem je znan kot Graham-ov algoritem.
Vhodni podatek je niz točk N, za katerega je potrebno ugotoviti
mejo konveksne lupine. Ideja temelji na izbiri neke poljubne točke
x v notranjosti meje mnogkotnika in ureditvi vseh točk
niza N po naraščujočem relativnem kotu v nasprotni smeri
urinih kazalcev (Slika 3.3).
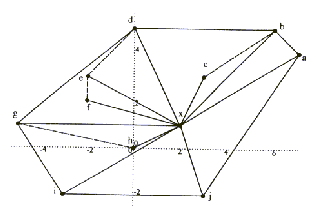
Slika 3.3 Točka 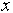 je poljubna;
je poljubna; 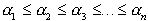 .
.
Naslednji korak je pregledovanje točk. Prvi točki niza S,
ki določa mejo konveksne lupine, sta 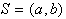 .
Naslednja točka, ki sledi po redu naraščujočih kotov, je točka
c. Ker naredi hodec na poti a,b,c v točki b
zavoj v levo, je b gotovo izbočeno teme in točka c
se pripiše nizu
.
Naslednja točka, ki sledi po redu naraščujočih kotov, je točka
c. Ker naredi hodec na poti a,b,c v točki b
zavoj v levo, je b gotovo izbočeno teme in točka c
se pripiše nizu 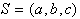 . Naslednjo je potrebno
preveriti točko d. Na poti b,c,d v temenu c
naredi hode zavoj v desno. To pomeni, da je c vbočeno teme
in kot tako ne more biti del konveksne lupine. Točka c
se iz niza S izbriše, vpiše se točka d,
. Naslednjo je potrebno
preveriti točko d. Na poti b,c,d v temenu c
naredi hode zavoj v desno. To pomeni, da je c vbočeno teme
in kot tako ne more biti del konveksne lupine. Točka c
se iz niza S izbriše, vpiše se točka d, 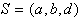 .
Ta postopek se ponavlja, dokler v nizu S prvi in zadnji
element nista enaka;
.
Ta postopek se ponavlja, dokler v nizu S prvi in zadnji
element nista enaka; 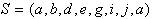 .
.
Glavni problem je, da ni moč z gotovostjo trditi, da sta točki a in b na konveksni lupini. Tako bi se v primeru, da nista, postopek preverjanja nadaljeval naprej, kljub temu, da je bil pregledan že ves niz N. Med začetkom in koncem niza S ne bi bilo logične povezave.
Problem nastane tudi v primeru, če je že v prvem koraku, pri trojici
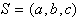 , ugotovljeno, da je v temenu b
obrat na desno. To pomeni, da je b nedvoumno vbočeno teme
in kot tako ne more biti del niza S. V tem primeru je potrebno
b iz niza
, ugotovljeno, da je v temenu b
obrat na desno. To pomeni, da je b nedvoumno vbočeno teme
in kot tako ne more biti del niza S. V tem primeru je potrebno
b iz niza 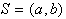 zbrisati. Ostane samo
zbrisati. Ostane samo
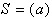 . Z eno samo točke naslednje ni mogoče
preverjati, potrebni sta najmanj dve.
. Z eno samo točke naslednje ni mogoče
preverjati, potrebni sta najmanj dve.
Rešitev je, če se za naključno točko x izbere najnižjo
(po koordinati y) točko niza N. Če sta taki točki
dve, je izbrana najbolj desna, najnižja točka niza N. Zaporedno
urajanje po naraščujočih kotih je enako kot prej omenjeno. Glede
na velikost relativnega kota naj bodo točke označena s 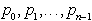 v nasprotni smeri urinih kazalcev. V tem primeru je logično,da
so točke
v nasprotni smeri urinih kazalcev. V tem primeru je logično,da
so točke 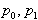 in
in 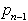 nedvoumno na konveksn lupini. S tem sta odpravljena oba prej omenjena
problema. Novo označevanje in urejanje je kot na sliki 3.4.
nedvoumno na konveksn lupini. S tem sta odpravljena oba prej omenjena
problema. Novo označevanje in urejanje je kot na sliki 3.4.
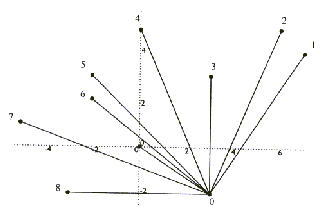
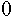 ,
(na sliki 2.4 točka i).
,
(na sliki 2.4 točka i).
Prvi naključni algoritem temelji na dodajanju polprostorov 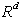 ,
v tem primeru polravnin
,
v tem primeru polravnin 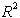 , v
, v 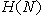 .
.
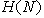 predstavlja presek vseh polravnin. Polravnina
je najosnovnejša konveksna lupina. Presek konveksnih lupin da
vedno novo konveksno lupino. Presek polravnin je torej konveksna
lupina.
predstavlja presek vseh polravnin. Polravnina
je najosnovnejša konveksna lupina. Presek konveksnih lupin da
vedno novo konveksno lupino. Presek polravnin je torej konveksna
lupina.
Naj bo N niz polravnin in 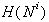 konveksna
lupina, t.j. presek vseh polravnin po dodani polravnini
konveksna
lupina, t.j. presek vseh polravnin po dodani polravnini 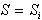 .
Naslednji korak je dodajanje
.
Naslednji korak je dodajanje 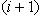 . polravnine
. polravnine
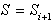 k
k 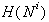 (Slika 3.5).
(Slika 3.5).
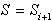 k
k 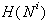 .
.
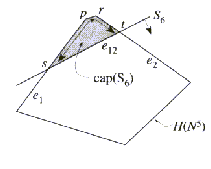
Razvrstitev 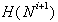 bo nastala iz
bo nastala iz 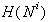 po odstranitvi kape
po odstranitvi kape 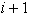 , ki je presek
, ki je presek 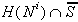 ,
pri čemer je polravnina
,
pri čemer je polravnina 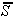 komplementarna
polravnini S (Slika 3.5). Najprej je potrebno izbrati poljubno
teme
komplementarna
polravnini S (Slika 3.5). Najprej je potrebno izbrati poljubno
teme 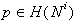 , ki leži na komplementarni ravnini
, ki leži na komplementarni ravnini
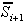 (Slika 3.5). Če tako teme ne obstaja,
se lahko ravnino
(Slika 3.5). Če tako teme ne obstaja,
se lahko ravnino 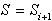 (Slika 3.5) izpusti,
saj ne vpliva na
(Slika 3.5) izpusti,
saj ne vpliva na 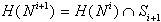 . Če tako teme obstaja,
je potrebno pregledati robove
. Če tako teme obstaja,
je potrebno pregledati robove 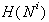 in ugotoviti
presečišči (vedno sta dve) med
in ugotoviti
presečišči (vedno sta dve) med 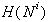 in mejo
polravnine
in mejo
polravnine 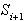 (oziroma
(oziroma 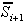 ).
).
Pregledovanje 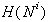 se začne v temenu p.
Naj bo f prvi rob, ki ga je potrebno pregledati. Če f
v celoti leži na polravnini
se začne v temenu p.
Naj bo f prvi rob, ki ga je potrebno pregledati. Če f
v celoti leži na polravnini 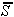 , potem ga
je potrebno s pripadajočima temenoma odstraniti. Prvi rob f,
ki leži na
, potem ga
je potrebno s pripadajočima temenoma odstraniti. Prvi rob f,
ki leži na 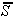 samo delno, je hkrati tudi
zadnji, ki ga je potrebno pregledati v tej smeri. Ta rob f
se razdeli na dva dela tako, da se tistega, ki leži na
samo delno, je hkrati tudi
zadnji, ki ga je potrebno pregledati v tej smeri. Ta rob f
se razdeli na dva dela tako, da se tistega, ki leži na 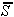 ,
izbriše, druga polovica pa je hkrati del
,
izbriše, druga polovica pa je hkrati del 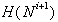 .
Pregledovanje je potrebno ponoviti tudi v drugi smeri, da se ugotovi
še drugi rob, ki leži hkrati na polravninah
.
Pregledovanje je potrebno ponoviti tudi v drugi smeri, da se ugotovi
še drugi rob, ki leži hkrati na polravninah 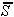 in S. Od
in S. Od 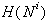 je potrebno odstraniti
še kapo, del
je potrebno odstraniti
še kapo, del 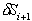 , ki leži med obema odrezanima
robovoma f, ki postaneta nova robova
, ki leži med obema odrezanima
robovoma f, ki postaneta nova robova 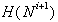 .
.
Drugi naključni algoritem je prav tako kot prejšnji inkrementalen, vendar gre v tem primeru za dodajanje točk (prejšnji primer polravnine). Algoritem je uporaben tudi pri vijših dimenzijah, pri konstruiranju konveksnih lupin v 3D, kar je eno pomembnejših področij računske geometrije.
Osnovna ideja je dodajanje točk ene za drugo h konveksni lupini,
ki jo že določa prvih k dodanih točk oziroma dodajanje
točke k obstoječi konveksni lupini. Naj bo 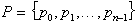 niz točk na ravnini. Prva konveksna lupina je trikotnik, sestavljen
iz
niz točk na ravnini. Prva konveksna lupina je trikotnik, sestavljen
iz 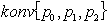 . Naj bo
. Naj bo 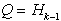 in
in
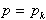 . Določanje konveksne lupine
. Določanje konveksne lupine 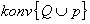 se razširi na dve možnosti v odvisnosti ali
se razširi na dve možnosti v odvisnosti ali 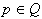 ali
ali 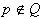 :
:
1. 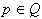 . Če je ugotovljeno, da leži
točka p v Q, potem jo lahko izpustimo, saj ne vpliva
na obliko konveksne lupine. Isto velja, če točka p leži
na meji Q t.j. Q. Za določanje notranjosti oziroma
zunanjosti se uporabi že omenjena t.i. predpostavko levega (2.4.1).
Za vsak rob konveksne lupine Q posebej se preverja ali
je točka na njegovi levi strani. Če to velja preko cele Q,
potem je p v notrajnosti Q.
. Če je ugotovljeno, da leži
točka p v Q, potem jo lahko izpustimo, saj ne vpliva
na obliko konveksne lupine. Isto velja, če točka p leži
na meji Q t.j. Q. Za določanje notranjosti oziroma
zunanjosti se uporabi že omenjena t.i. predpostavko levega (2.4.1).
Za vsak rob konveksne lupine Q posebej se preverja ali
je točka na njegovi levi strani. Če to velja preko cele Q,
potem je p v notrajnosti Q.
2. 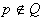 . Če se za katerikoli rob izkaže,
da predpostavka levega ne drži, potem velja
. Če se za katerikoli rob izkaže,
da predpostavka levega ne drži, potem velja 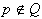 in mogoča je določitev
in mogoča je določitev 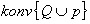 . Potrebno je poiskati
dve tangenti, ki povezujeta p s Q in oblikovati
novo konveksno lupino (Slika 3.6).
. Potrebno je poiskati
dve tangenti, ki povezujeta p s Q in oblikovati
novo konveksno lupino (Slika 3.6).
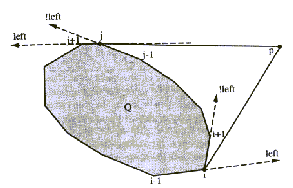
Slika 3.6 Tangenti od p h Q; "levo"
pomeni, da je p levo od nakazane smeri in "!levo",
da p ni levo od nakazane smeri.
Tangenta, ki povezuje p s Q, se meje konveksne lupine
Q dotika v eni sami točki. Naj bo p ena izmed takih
točk. Kako se določi 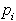 ? Tudi v tem primeru
je uporabna predpostavka levega. Na Sliki 3.6 je vidno, da je
točka
? Tudi v tem primeru
je uporabna predpostavka levega. Na Sliki 3.6 je vidno, da je
točka 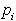 levo od smeri
levo od smeri 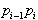 in desno oziroma nelevo od smeri
in desno oziroma nelevo od smeri 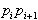 . Za
zgornjo tangento velja ravno obratno;
. Za
zgornjo tangento velja ravno obratno; 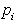 desno od smeri
desno od smeri 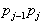 in levo od smeri
in levo od smeri 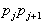 .
Sledi, da je
.
Sledi, da je 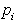 točka tangente, če se za
dve sosednji točki dobi različen rezultat predpostavke levega.
Ostane še konstrukcija nove konveksne lupine, ki je
točka tangente, če se za
dve sosednji točki dobi različen rezultat predpostavke levega.
Ostane še konstrukcija nove konveksne lupine, ki je 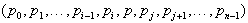 .
.
Na naslednji stopnji imamo opraviti s konveksnimi lupinami v tridimenzionalnem
prostoru. V dvodimenzionalnem prostoru je konveksna lupina določena
kot množica točk na ravnini (teme), ki so med seboj povezane z
linijskimi segmenti (robovi) po določenih definicijskih pravilih.
Tudi v treh dimenzijah konveksno lupino določa množica točk v
prostoru (teme), ki so med seboj povezane z linijskimi segmenit
(robovi), ti pa med seboj s ploskvami, po določenih definicijskih
pravilih. Temena robov so hkrati tudi temena ploskev. Podobno,
kot je lupina v 2D določena kot presek polravnin 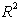 ,
je konveksna lupina v 3D določena kot presek polprostorov
,
je konveksna lupina v 3D določena kot presek polprostorov 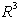 .
.
Polieder je naravno posploševanje dvodimenzijskega mnogokotnika v tri dimenzije: je območje v prostoru, katerega meja vsebuje končno število večstranih ploskev, ki so lahko nepovezane, ali pa se med seboj dotikajo v robovih in temenih. Ta definicija je precej nejasna, še posebno, kadar ima opraviti z lupinami na splošmo.
Meja poliedra je sestavljena iz treh vrst geometrijskih objektov:
ničdimenzijskih temen (točke), enodimenzijskih robov (linijski
segmenti) in dvodimenzijskih površin (mnogokotniki). Površino
poliedra se lahko podrobno označi z odnosi med posameznimi geometrijskimi
objekti. Pri tem so upoštevani trije pogoji: objekti se morajo
med seboj sekati "pravilno", lokalna topologija mora
biti "pravilna", globalna topologija mora biti "pravilna".
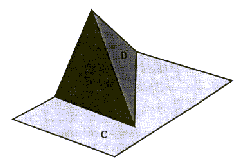
1. Objekti se sekajo "pravilno".
Za vsak par ploskev se zahteva, ali
(a) se med seboj ne dotikata, ali
(b) imata eno skupno teme, ali
(c) imata dve skupni temeni in en skupen rob, ki ti dve temeni
povezuje med seboj.
Nepravilno sekanje je torej prediranje ploskev in napačno dotikanje
ploskev med seboj (Slika 3.7). S tem, ko so določena presečišča
med ploskvami, so določena tudi presečišča med robovi in temeni.
2. Lokalna topologija je "pravilna".
Lokalna topologija popisuje površino v okolici točke. Tehnično
se ta omejenost popiše, da naj bo okolica vsake točke na površini
homeomorfična disku. Homeomorfičnost dopušča raztezanje in upogibanje,
ne dopušča pa pretrganja (Slika 3.8).
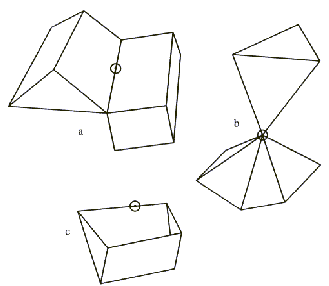
Slika 3.8 Ti trije objekti niso poliedri. V vseh treh primerih
okolica točke ni homeomorfična disku: (a) točka leži hkrati na
dveh ploskvah; (b) triangulacija ne da enostavno zaprte povezave
med elementi; (c) objekt ni zaprt, okolica točke je pol disk.
3. Globalna topologija je "pravilna".
Površina mora biti zvezna, zaprta in omejena. To pomeni, da namišljeni
hodec lahko prehodil katerokoli pot med katerikolima točkama na
tej površini. V tem smislu so dovoljeni tuneli oziroma različne
udrtine v lupino. Obravnavanje konveksnih lupin teh dveh pojvov
ne zajema.
Upoštevaje vse skupaj sledi: meja poliedra je končen zbir ravninskih,
konveksnih, omejenih mnogokotnikov na način, da:
1. se ploskve sekajo pravilno,
2 da je okolica vsake točke homeomorfična oblika diska oziroma, da je povezava med temeni preprosta mnogokotna veriga,
3. da jepovršina zvezna.
Meja je torej zaprta in obdaja oziroma omejuje območje prostora.
Vsak rob si delita natančno dve ploskvi; imenujemo ju sosednji.
Za konveksen polieder velja, da je segment, ki povezuje katerikoli
točki poliedra, v notranjosti tega poliedra. Konveksnost je popisljiva
tudi z notranjimi koti. Notranji kot med dvema sosednjima ploskvama
je vedno 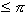 in vsota vseh takih kotov okoli
vsakega temena je
in vsota vseh takih kotov okoli
vsakega temena je 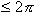 .
.
Pravini poliedri so tisti, katerih ploskve so skladni, pravilni
mnogokotniki: enakostraničen trikotnik, kvadrat, pravilni petkotnik,
itd. Število ploskev, ki se stikajo v enem temenu je enako za
vsa temena pravilnega poliedra. Obstaja samo pet značilno pravilnih
poliedrov. Če je p število temen na ploskev in v
število ploskev, ki se dotikajo v temenu, mora za pravilni polieder
veljati 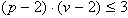 (Slika 3.9).
(Slika 3.9).
Tabela 3.1: Seznam vrednosti 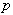 in
in
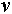 .
.
| p | v | (p-2)(v-2) | ime | opis |
| 3 | 3 | 1 | tetraeder | trije trikotniki na teme |
| 4 | 3 | 2 | kocka | trije kvadrati na teme |
| 3 | 4 | 2 | oktaeder | štirje trikotniki na teme |
| 5 | 3 | 3 | dodekaeder | trije petkotniki na teme |
| 3 | 5 | 3 | ikozaeder | pet trikotnikov na teme |

Medsebojen odnos med številom temen, robov in ploskev popisuje Euler-jeva formula
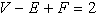 (Tabela 3.2).
(Tabela 3.2).
Tabela 3.2: Število temen,
robov in ploskev petih pravilnih poliedrov.
| Ime | (p, v) | V | E | F |
| tetraeder | (3, 3) | 4 | 6 | 4 |
| kocka | (4, 4) | 8 | 12 | 6 |
| oktaeder | (3, 4) | 6 | 12 | 8 |
| dodekaeder | (5, 3) | 20 | 30 | 12 |
| ikozaeder | (3, 5) | 12 | 30 | 20 |
Iz množice točk je mogoče določiti polieder s pomočjo inkrementalnega
algoritma. Že opisani je zadostoval za konstrukcijo konveksne
lupine iz množice točk na ravnini, naslednji pa omogoča konstruiranje
konveksne lupine iz množice točk v prostoru.
Glavna ideja je identična: pri i-tem dodajanju točke je
potrebno določiti 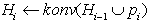 . Problem določanja
se razdeli na dva dela. Naj bo
. Problem določanja
se razdeli na dva dela. Naj bo 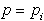 in
in 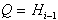 .
Ugotoviti je potrebno, če velja
.
Ugotoviti je potrebno, če velja 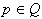 . Če to
drži, se lahko točko p izpusti, če ne, je potrebno določiti
'stožec', ki je tangenten na Q in ima vrh v točki p
ter skonstruirati novo konveksno lupino. Test
. Če to
drži, se lahko točko p izpusti, če ne, je potrebno določiti
'stožec', ki je tangenten na Q in ima vrh v točki p
ter skonstruirati novo konveksno lupino. Test 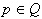 se izvede podobno kot v dveh dimenzijah. Točka p je v notranjost
Q, če je p na pozitivni strani vsake izmed ploskev,
ki določajo lupino Q. Testiranje predpostavke levega omogoča
volumen tetraedra, kakor to pri dveh dimenzijah omogoča površina
trikotnika. Če je točka p v notranjosti lupine Q,
morajo imeti vsi volumni enak predznak. Problem nastane kadar
je točka zunaj lupine Q, saj je potrebno le to spremeniti.
se izvede podobno kot v dveh dimenzijah. Točka p je v notranjost
Q, če je p na pozitivni strani vsake izmed ploskev,
ki določajo lupino Q. Testiranje predpostavke levega omogoča
volumen tetraedra, kakor to pri dveh dimenzijah omogoča površina
trikotnika. Če je točka p v notranjosti lupine Q,
morajo imeti vsi volumni enak predznak. Problem nastane kadar
je točka zunaj lupine Q, saj je potrebno le to spremeniti.
V ravninskem primeru je bilo potrebno poiskati dve tangenti med
točko p in lupino Q. V prostoru pa tangentne linije
zamenjajo tangentne ploskve. Te ploskve skupaj oblikujejo stožčasto
telo, ki je sestavljeno iz trikotnih ploskev, katerih skupni vrh
je v točki p, osnova pa rob e na lupini Q.
Če bi iz točke p pogledali proti Q bi ugotovili,
da je nekaj ploskev Q vidnih, nekaj pa nevidnih. Vse tiste
ploskve, ki so vidne je potrebno izbrisati pri spreminjanju 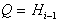 v
v 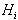 . Robovi vidnosti postanejo osnova za
konstrukcijo stožca z vrhom v točki p. Rob e na
lupini Q je torej tak rob, da je ploskev, ki povezuje e
s p, tangnta na Q. Rob e je sosedenj dvema
ploskvama. Ena teh je iz točke p vidna, druga ni. Rob e
je torej na meji vidnega dela.
. Robovi vidnosti postanejo osnova za
konstrukcijo stožca z vrhom v točki p. Rob e na
lupini Q je torej tak rob, da je ploskev, ki povezuje e
s p, tangnta na Q. Rob e je sosedenj dvema
ploskvama. Ena teh je iz točke p vidna, druga ni. Rob e
je torej na meji vidnega dela.
Podobno se lahko točko p privzame kot izvor svetlobe. Del lupine Q bo osvetljen, del pa bo ostal v senci. Rob e je tista linija, ki ločuje osvetljeni del od senčnega.
V nadaljevanju algoritma je potrebno poiskati vse ploskve, ki
so vidne iz točke p. To se ugotovi s pomočjo volumna, ki
ga določajo točke na lupini Q, to so (a,b,c)
in točka p. Če je ploskev (a,b,c) iz točke p
vidna, potem je volumen tetraedra (a,b,c,p) nedvoumno negativen.
Taka ploskev se odstrani, 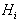 pa se oblikuje
iz nevidnega dela lupine in ploskovne povezave med mejnim robom
e in točko p. V naslednjem koraku se izbere novo
točko in ves postopek preverjanja in ponovnega konstruiranja se
ponovi, dokler ni pregledanih vseh n točk niza N
v prostoru.
pa se oblikuje
iz nevidnega dela lupine in ploskovne povezave med mejnim robom
e in točko p. V naslednjem koraku se izbere novo
točko in ves postopek preverjanja in ponovnega konstruiranja se
ponovi, dokler ni pregledanih vseh n točk niza N
v prostoru.
Osnovni algoritem za računalniško konstrukcijo lupine v 3D iz
niza točk je prikazan v Algoritmu 3.1.
Algoritem: Tridimenzionalni inkrementalni alhoritem
Pripisati for i=4,...,n-1 do
for za vsako ploskev f stopnje
Izračun volumna tetraedra določenega z f in f je vidna, če je prostornina 0. če ni nobene ploskve vidne
then izločiti else
for za vsak mejni rob e stopnje
Konstrukcija ploskve, ki jo določata rob e in točka for za vsako vidno ploskev f do Briši f.
Popravi |
V višjih dimenzijah postanejo problemi bolj zapleteni
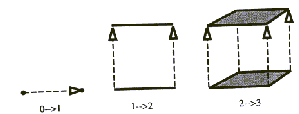
in težje predtavljivi. Hiperprostor si je najlaže predstavljati,
če si znamo predstavljati preskoke iz ničdimenzijskega prostora
v enodimenzijski in naprej v dvo in trodimenzijski prostor.
Predstavljanje prve, druge in tretje dimenzije je preprosto. Problem
nastane pri višjih dimenzijah. Najboljši je postopen pristop skozi
nižje dimenzije. Točka na številski premici je predstavljena z
eno samo številko: je vrednost oziroma lokacija. Lahko jo upoštevamo
kot enodimenzijski objekt, saj leži na premici, ki je enodimenzijski
element. Točka v dveh dimenzijah je določljiva z dvema koordinatama
(x,y), v treh dimenzijah pa s tremi (x,y,z).
Iz tega sledi, da so za točko v štirih dimenzijah potrebne štiri
koordinate (x,y,z,t). Če prve tri
koordinate (x,y,z) razumemo kot prostorske
koordinate in t kot čas, potem vse štiri skupaj predstavljajo
dogodek v prostoru in času. Poleg prostor-časa obstaja še več
možnih izpeljav višjih dimenzij. Ena med njimi je primer hiperkocke.
Ničdimenzionalna kocka je točka. Enodimenzionalna kocka je daljica.
Dvodimenzionalna kocka je kvadrat. Tridimenzionalna kocka je normalna
kocka v prostoru. Pri tem veljajo naslednji podatki:
| Ime | |||
| točka | |||
| daljica | |||
| kvadrat | |||
| kocka | |||
| hiperkocka | |||
| d-kocka |
V je število temn in E
število robov.
Kocka v d dimenzijah je zgrajena iz dveh kock
(druga je kopija prve) dimenzije d-1. Če imamo enodimenzijsko
kocko (točko) in jo raztegnemo v drugo dimenzijo, nastane dvodimenzijska
kocka, daljica. Če to naprej raztegnemo v smeri pravokotno sebi,
nastane kvadrat. Če preslikamo kvadrat na ravnino, ki je vzporedna
prvi, nastane kocka. Če kocko z osmimi temeni in dvanajstimi robovi
preslikamo v nov položaj in obe kocki povežemo z osmimi robovi,
dobimo t.i. hiperkocko. To je kocka v četrti dimenziji. Koordinate
temen, vseh je šestnajst, predstavljajo konveksno lupino.